
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Reduce and scan are core primitives of parallel computing. These simple implementations are compact for maximum legibility, but also support user-defined types and operators.

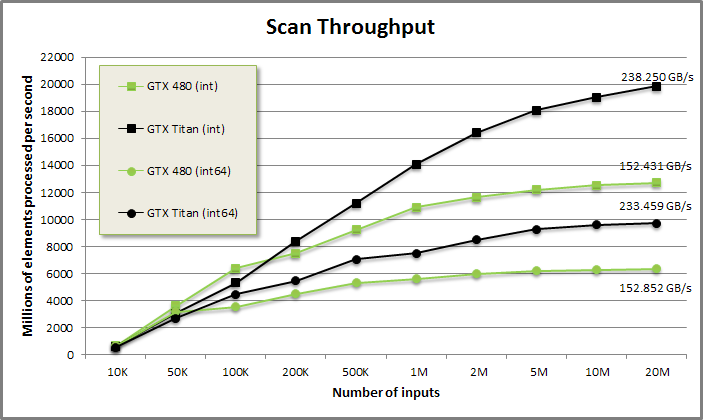
Scan benchmark from benchmarkscan/benchmarkscan.cu
Scan demonstration from demo/demo.cu
void DemoScan(CudaContext& context) {
printf("\n\nREDUCTION AND SCAN DEMONSTRATION:\n\n");
// Generate 100 random integers between 0 and 9.
int N = 100;
MGPU_MEM(int) data = context.GenRandom<int>(N, 0, 9);
printf("Input array:\n");
PrintArray(*data, "%4d", 10);
// Run a global reduction.
int total = Reduce(data->get(), N, context);
printf("Reduction total: %d\n\n", total);
// Run an exclusive scan.
ScanExc(data->get(), N, &total, context);
printf("Exclusive scan:\n");
PrintArray(*data, "%4d", 10);
printf("Scan total: %d\n", total);
}REDUCTION AND SCAN DEMONSTRATION:
Input array:
0: 8 1 9 8 1 9 9 2 6 3
10: 0 5 2 1 5 9 9 9 9 9
20: 1 7 9 9 9 1 4 7 8 2
30: 1 0 4 1 9 6 7 8 9 5
40: 6 7 0 3 8 2 9 6 6 3
50: 7 7 7 4 3 4 6 1 1 3
60: 7 7 0 3 2 8 0 1 0 9
70: 8 8 6 1 3 7 9 4 0 6
80: 4 1 3 2 7 0 7 0 1 4
90: 4 4 4 4 6 7 7 9 7 8
Reduction total: 492
Exclusive scan:
0: 0 8 9 18 26 27 36 45 47 53
10: 56 56 61 63 64 69 78 87 96 105
20: 114 115 122 131 140 149 150 154 161 169
30: 171 172 172 176 177 186 192 199 207 216
40: 221 227 234 234 237 245 247 256 262 268
50: 271 278 285 292 296 299 303 309 310 311
60: 314 321 328 328 331 333 341 341 342 342
70: 351 359 367 373 374 377 384 393 397 397
80: 403 407 408 411 413 420 420 427 427 428
90: 432 436 440 444 448 454 461 468 477 484
Scan total: 492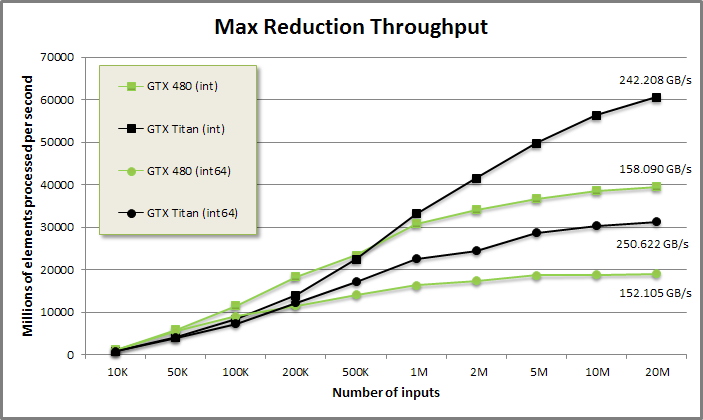
Max-reduce benchmark from benchmarkscan/benchmarkscan.cu
Max scan and reduce demonstration from demo/demo.cu
void DemoMaxReduce(CudaContext& context) {
printf("\n\nMAX-REDUCE DEMONSTRATION:\n\n");
// Generate 100 random integers between 0 and 999.
int N = 100;
MGPU_MEM(int) data = context.GenRandom<int>(N, 0, 999);
printf("Input array:\n");
PrintArray(*data, "%4d", 10);
// Run a max inclusive scan.
MGPU_MEM(int) scan = context.Malloc<int>(N);
Scan<MgpuScanTypeInc>(data->get(), N, INT_MIN, mgpu::maximum<int>(),
(int*)0, (int*)0, scan->get(), context);
printf("\nInclusive max scan:\n");
PrintArray(*scan, "%4d", 10);
// Run a global reduction.
int reduce;
Reduce(data->get(), N, INT_MIN, mgpu::maximum<int>(), (int*)0, &reduce,
context);
printf("\nMax reduction: %d.\n", reduce);
}MAX-REDUCE DEMONSTRATION:
Input array:
0: 276 705 679 2 655 710 162 643 118 456
10: 498 773 959 573 340 876 585 808 223 17
20: 751 821 255 820 505 940 699 412 890 423
30: 959 580 547 158 138 761 149 230 257 809
40: 840 988 254 332 814 299 243 13 929 217
50: 349 907 196 848 251 955 616 778 473 987
60: 351 67 830 793 585 594 549 732 917 695
70: 285 679 757 392 753 561 380 208 567 527
80: 75 404 53 352 530 592 779 356 934 964
90: 129 154 568 394 469 387 11 726 337 388
Inclusive max scan:
0: 276 705 705 705 705 710 710 710 710 710
10: 710 773 959 959 959 959 959 959 959 959
20: 959 959 959 959 959 959 959 959 959 959
30: 959 959 959 959 959 959 959 959 959 959
40: 959 988 988 988 988 988 988 988 988 988
50: 988 988 988 988 988 988 988 988 988 988
60: 988 988 988 988 988 988 988 988 988 988
70: 988 988 988 988 988 988 988 988 988 988
80: 988 988 988 988 988 988 988 988 988 988
90: 988 988 988 988 988 988 988 988 988 988
Max reduction: 988.////////////////////////////////////////////////////////////////////////////////
// kernels/reduce.cuh
// Reduce input and return variable in device memory or host memory, or both.
// Provide a non-null pointer to retrieve data.
template<typename InputIt, typename T, typename Op>
MGPU_HOST void Reduce(InputIt data_global, int count, T identity, Op op,
T* reduce_global, T* reduce_host, CudaContext& context);
// T = std::iterator_traits<InputIt>::value_type.
// Reduce with Op = ScanOp<ScanOpTypeAdd, T>.
template<typename InputIt>
MGPU_HOST typename std::iterator_traits<InputIt>::value_type
Reduce(InputIt data_global, int count, CudaContext& context);
////////////////////////////////////////////////////////////////////////////////
// kernels/scan.cuh
// Scan inputs in device memory.
// MgpuScanType may be:
// MgpuScanTypeExc (exclusive) or
// MgpuScanTypeInc (inclusive).
// Return the total in device memory, host memory, or both.
template<MgpuScanType Type, typename InputIt, typename T, typename Op,
typename DestIt>
MGPU_HOST void Scan(InputIt data_global, int count, T identity, Op op,
T* reduce_global, T* reduce_host, DestIt dest_global,
CudaContext& context);
// Exclusive scan with identity = 0 and op = mgpu::plus<T>.
// Returns the total in host memory.
template<typename InputIt, typename TotalType>
MGPU_HOST void ScanExc(InputIt data_global, int count, TotalType* total,
CudaContext& context);
// Like above, but don't return the total.
template<typename InputIt>
MGPU_HOST void ScanExc(InputIt data_global, int count, CudaContext& context);Further Reading: For a detailed introduction to reduction networks read NVIDIA's Mark Harris on Optimizing Parallel Reduction in CUDA.
Reduce and scan (prefix sum) are core primitives in parallel computing. Reduce is the sum of elements in an input sequence:
Input: 1 7 4 0 9 4 8 8 2 4 5 5 1 7 1 1 5 2 7 6 Reduction: 87
Scan generalizes this operator, reducing inputs for every interval from the start to the current element. Exclusive scan is the sum of all inputs from the beginning to the element before the current element. Inclusive scan is the exclusive scan plus the current element. You can convert from inclusive to exclusive scan with a component-wise subtraction of the input array, or by shifting the scan one element to the right:
Input: 1 7 4 0 9 4 8 8 2 4 5 5 1 7 1 1 5 2 7 6 Exclusive: 0 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 72 74 81 Inclusive: 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 72 74 81 87
Note that the last element of inclusive scan is the reduction of the inputs.
Parallel evaluation of reduce and scan requires cooperative scan networks which sacrifice work efficiency to expose parallelism.
For reduction, we recursively fold values together:
Input: 1 7 4 0 9 4 8 8 2 4 5 5 1 7 1 1 5 2 7 6
Reduce progress by pass:
1: 1 7 4 0 9 4 8 8 2 4 +
5 5 1 7 1 1 5 2 7 6
6 12 5 7 10 5 13 10 9 10
2: 6 12 5 7 10 +
5 13 10 9 10
11 25 15 16 20
3: 11 25 15 +
16 20
11 41 35
4: 11 41 +
35
11 76
4: 11 +
76
87
On the first pass, each thread in the left half of the CTA loads its corresponding value on the right half of the CTA, adds it into its own value, and stores the result back. On the second pass, the first quarter of the threads load values for the next quarter, add, and store. This is repeated log(N) times until all values in the tile have been folded together. The number of additions is still N-1 in this parallel implementation, although there is a loss of efficiency due to branch divergence when the number of active lanes is less than one warp's width.
This implementation of reduction requires both associativity and commutativity in the operator. Although commutativity can be relaxed by re-ordering inputs, associativity is generally required for all parallel computation.
Consider the cooperative scan network based on the Kogge-Stone adder. n inputs are processed in log(n) passes. On pass 0, element i - 1 (if in range) is added into element i, in parallel. On pass 1, element i - 2 is added into element i. On pass 2, element i - 4 is added into element i, and so on.
Input: 1 7 4 0 9 4 8 8 2 4 5 5 1 7 1 1 5 2 7 6 Inclusive scan network by offset: 1: 1 8 11 4 9 13 12 16 10 6 9 10 6 8 8 2 6 7 9 13 2: 1 8 12 12 20 17 21 29 22 22 19 16 15 18 14 10 14 9 15 20 4: 1 8 12 12 21 25 33 41 42 39 40 45 37 40 33 26 29 27 29 30 8: 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 71 66 69 75 16: 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 72 74 81 87 Exclusive: 0 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 72 74 81
On each pass, the element in red (column 17 - offset) is added into the element in green (column 17) and stored at column 17 on the next line. By the last pass this chain of adders has communicated the sum of all elements between columns 0 and 16 into column 17.
The sequential implementation runs in O(n) operations with O(n) latency. The parallel version has O(n log n) work efficiency, but by breaking the serial dependencies, improves latency to O(log n) on machines with n processors.
Most workloads have many more inputs than the device has processors. Processing large inputs with the parallel reduce and scan networks described above is not practical, due to the required synchronization between each pass.
In the case of reduce, the parallel network requries more data movement than an optimal implementation. In the case of scan, the parallel network requires both more data movement and more computation, due to O(n log n) algorithmic complexity for an operation that should be linear.
We use register blocking to improve work-efficiency and reduce synchronization. This general parallel-computing strategy assigns multiple values to each thread, which are processed sequentially. Each thread's local reduction may then be processed with a parallel reduce or scan network, or fed back into a function that again processes inputs with register blocking.
Nearly all Modern GPU routines are register blocked. The number of values assigned to a thread is the grain size, which we refer to as VT (values per thread). Grain size becomes the primary tuning parameter for finding optimal performance on each GPU architecture:
Increasing grain size does more sequential processing per thread, improving overall work-efficiency, but also uses more per-thread state, reducing occupancy and compromising the device's ability to hide latency.
Decreasing grain size does less sequential processing per thread, decreasing overall work-efficiency, but also uses less per-thread state, increasing occupancy and enabling the device to better hide latency.
Register blocking with scan leads results in a common three-phase process. The use of sequential operations in this parallel algorithm are called "raking reductions" and "raking scans," because they are computed within lanes rather than cooperatively over the lanes.
Upsweep to send partial reductions to the spine. Each CTA/thread sequentially reduces its assignment of inputs and stores to global/shahred memory. This is the carry-out value for the CTA/thread.
Scan the spine of partials. Exclusive scan the carry-out values produced in step 1. This turns carry-out values into carry-in values.
Downsweep to distribute scanned partials from the spine to each of the inputs. Each CTA/thread sequentially scans its assignment of inputs, adding the carry-in (the output of step 2) into each scanned value.
Register blocking with reduce requires only repeated application of the upsweep phase until all values are folded into one carry-out.
Input array: 20 threads and 5 elements/thread:
1 7 4 0 9 4 8 8 2 4 5 5 1 7 1 1 5 2 7 6
1 4 2 3 2 2 1 6 8 5 7 6 1 8 9 2 7 9 5 4
3 1 2 3 3 4 1 1 3 8 7 4 2 7 7 9 3 1 9 8
6 5 0 2 8 6 0 2 4 8 6 5 0 9 0 0 6 1 3 8
9 3 4 4 6 0 6 6 1 8 4 9 6 3 7 8 8 2 9 1
Partial reduction by threads (Upsweep):
21 26 19 21 12 22 31 27 12 17 27 30 21 20 20 18 26 21 29 28
Parallel scan of partials (Spine):
1: 21 47 45 40 33 34 53 58 39 29 44 57 51 41 40 38 44 47 50 57
2: 21 47 66 87 78 74 86 92 92 87 83 86 95 98 91 79 84 85 94 104
4: 21 47 66 87 99 121 152 179 170 161 169 178 187 185 174 165 179 183 185 183
8: 21 47 66 87 99 121 152 179 191 208 235 265 286 306 326 344 349 344 354 361
16: 21 47 66 87 99 121 152 179 191 208 235 265 286 306 326 344 370 391 420 448
Exclusive scan of partials:
0 21 47 66 87 99 121 152 179 191 208 235 265 286 306 326 344 370 391 420
Add exclusive scan of partials into exclusive sequential scan of input array (Downsweep):
0 1 8 12 12 21 25 33 41 43 47 52 57 58 65 66 67 72 74 81
87 88 92 94 97 99 101 102 108 116 121 128 134 135 143 152 154 161 170 175
179 182 183 185 188 191 195 196 197 200 208 215 219 221 228 235 244 247 248 257
265 271 276 276 278 286 292 292 294 298 306 312 317 317 326 326 326 332 333 336
344 353 356 360 364 370 370 376 382 383 391 395 404 410 413 420 428 436 438 447The figure above illustrates the raking scan pattern, using 20 threads to cooperatively scan 100 inputs. During the upsweep phase, each thread reduces five inputs using a work-efficient serial loop. The 20 partials are then scanned in parallel using five parallel scan passes. During the downsweep phase, each thread sequentially adds its five inputs into the scanned partial from the spine. By increasing the grain size (the parameter VT in MGPU kernels) we do more linear-complexity work to amortize the O(n log n) scan network cost.
The previous update defined a scan op interface with several typedefs and four methods. It also supported operators that were commutative (high-speed, preferred) and non-commutative. This allowed for maximum flexibility. The new update removes this complicated interface and replaces it with a simple functor object and an identity value.
template<typename T>
struct plus : public std::binary_function<T, T, T> {
MGPU_HOST_DEVICE T operator()(T a, T b) { return a + b; }
};
template<typename T>
struct minus : public std::binary_function<T, T, T> {
MGPU_HOST_DEVICE T operator()(T a, T b) { return a - b; }
};
template<typename T>
struct multiplies : public std::binary_function<T, T, T> {
MGPU_HOST_DEVICE T operator()(T a, T b) { return a * b; }
};
To use reduce or scan, define a class which inherits std::binary_function and implements a two-argument operator() method. These are device-compatible versions of std::plus, std::minus, etc.
Reduce and scan functions also require an identity argument. This value is arithmetically neutral with respect to the operator. The identity for mgpu::plus is 0; the identity for mpgu::multiplies is 1, etc. This term is not strictly requried for computing reduction or inclusive scan (exclusive scan needs it for the first element), but the MGPU library uses it to significantly simplify implementation.
template<int NT, int VT, typename InputIt, typename T> MGPU_DEVICE void DeviceGlobalToSharedDefault(int count, InputIt source, int tid, T* dest, T init, bool sync);
Rather than deal with the partial tile in a special branch, our implementations use DeviceGlobalToRegDefault or DeviceGlobalToSharedDefault to load any tile-sized intervals—partial tiles are padded with the identity. The same execution code is used on both full and partial tile CTAs.
Both MGPU and CUB encapsulate the storage requirements of a function with the function logic. While encapsulating data and methods (object-oriented programming) is generally not good practice for high-throughput parallel computing, binding storage with methods helps fully utilize on-chip storage.
template<int NT, typename Op = mgpu::plus<int> >
struct CTAReduce {
typedef typename Op::first_argument_type T;
enum { Size = NT, Capacity = NT };
struct Storage { T shared[Capacity]; };
template<int NT, typename Op = mgpu::plus<int> >
MGPU_DEVICE static T Reduce(int tid, T x, Storage& storage, Op op = Op()) {
...
Cooperative functions like reduction communicate their shared memory storage requirements by defining a Storage type in the enclosing class. Storage provisions space for storing one value per thread. The caller unions this into its own shared memory struct.
typedef CTAReduce<NT> R;
typedef CTAScan<NT> S;
union Shared {
KeyType keys[NT * (VT + 1)];
int indices[NV];
typename R::Storage reduceStorage;
typename S::Storage scanStorage;
};
__shared__ Shared shared;Shared memory is a critical resource and many kernels are performance-limited by shared memory capacity. We try to make the most-efficient use of shared memory by unioning together the encapsulated storage objects of each subroutine in the kernel.
As a rule of thumb, don't use shared memory to store data between calls. Use it for dynamic indexing and for inter-thread communication. The device subroutines in this library do not save or restore the contents of shared memory; they simply act as if they have exclusive access to the resource. Calls should not place data into shared memory expecting it to remain unmodified after invoking a device function that takes an encapsulated Storage parameter.
template<int NT, typename Op = mgpu::plus<int> >
struct CTAReduce {
typedef typename Op::first_argument_type T;
enum { Size = NT, Capacity = NT };
struct Storage { T shared[Capacity]; };
template<int NT, typename Op = mgpu::plus<int> >
MGPU_DEVICE static T Reduce(int tid, T x, Storage& storage, Op op = Op()) {
storage.shared[tid] = x;
__syncthreads();
// Fold the data in half with each pass.
#pragma unroll
for(int destCount = NT / 2; destCount >= 1; destCount /= 2) {
if(tid < destCount) {
// Read from the right half and store to the left half.
x = op(x, storage.shared[destCount + tid]);
storage.shared[tid] = x;
}
__syncthreads();
}
T total = storage.shared[0];
__syncthreads();
return total;
}
};CTAReduce::Reduce iteratively folds pairs of values together until the reduction is complete. Each thread begins by storing its input into shared memory. After the synchronization, we loop over destCount = NT / 2, NT / 4, ..., 1. At each iteration, thread tid loads the value from destCount + tid, adds it to its own value, and stores the result at slot tid. After the loop is complete, all threads load the reduced value and return.
To reduce latency we utilize the shfl ("shuffle") instruction available on Kepler. This feature implements inter-lane communication inside a warp with higher bandwidth than LD/ST pairs to shared memory. Although CUDA C++ includes a __shfl intrinsic, we choose to access the instruction using inline PTX to save the returned predicate flag. The current CUDA backend copies predicate flags into registers when they are returned as bool types, resulting in wasted instructions if we were to build a shuffle intrinsic that returned both value and predicate. The best performance is achieved by executing both the shfl and the add in inline PTX.
MGPU_DEVICE int shfl_add(int x, int offset, int width = WARP_SIZE) {
int result = 0;
#if __CUDA_ARCH__ >= 300
int mask = (WARP_SIZE - width)<< 8;
asm(
"{.reg .s32 r0;"
".reg .pred p;"
"shfl.up.b32 r0|p, %1, %2, %3;"
"@p add.s32 r0, r0, %4;"
"mov.s32 %0, r0; }"
: "=r"(result) : "r"(x), "r"(offset), "r"(mask), "r"(x));
#endif
return result;
}
The mov instruction is elided by the compiler, creating a warp scan in a tight sequence of five shfl and five predicated add instructions. The shfl_add function scans multiple segments within a warp, where width is a power-of-two segment size. The third argument of shfl_add guards against carry-in from a preceding segment—only values in the same segment are added in each pass.
#if __CUDA_ARCH__ >= 300
template<int NT>
struct CTAReduce<NT, mgpu::plus<int> > {
typedef mgpu::plus<int> Op;
typedef int T;
enum { Size = NT, Capacity = WARP_SIZE };
struct Storage { int shared[Capacity]; };
MGPU_DEVICE static int Reduce(int tid, int x, Storage& storage,
Op op = Op()) {
const int NumSections = WARP_SIZE;
const int SecSize = NT / NumSections;
int lane = (SecSize - 1) & tid;
int sec = tid / SecSize;
// In the first phase, threads cooperatively find the reduction within
// their segment. The segments are SecSize threads (NT / WARP_SIZE)
// wide.
#pragma unroll
for(int offset = 1; offset < SecSize; offset *= 2)
x = shfl_add(x, offset, SecSize);
// The last thread in each segment stores the local reduction to shared
// memory.
if(SecSize - 1 == lane) storage.shared[sec] = x;
__syncthreads();
// Reduce the totals of each input segment. The spine is WARP_SIZE
// threads wide.
if(tid < NumSections) {
x = storage.shared[tid];
#pragma unroll
for(int offset = 1; offset < NumSections; offset *= 2)
x = shfl_add(x, offset, NumSections);
storage.shared[tid] = x;
}
__syncthreads();
int reduction = storage.shared[NumSections - 1];
__syncthreads();
return reduction;
}
};
#endif // __CUDA_ARCH__ >= 300We specialize CTAReduce on the mgpu::plus<int> operator to accelerate this very common operation. An upsweep is implemented by reducing NumSections = WARP_SIZE sections, each of width SecSize = NT / WARP_SIZE. For an eight warp CTA (256 threads), there are NumWarps * log(SecSize) = 24 shfl_add invocations in the upsweep. The spine scan consists of 5 shfl_add calls, for 29 in all.
The shfl specialization runs faster than the general case in latency-limited kernels. A CTA with 256 threads requires eight folding passes in the general case, and similarly has a depth of eight shfl_add calls on warp 0 of the specialization. But in the specialization we replace costly load-store-synchronize sequences with faster shuffles, reducing the time to completion for warp 0.
template<typename Tuning, typename InputIt, typename T, typename Op>
MGPU_LAUNCH_BOUNDS void KernelReduce(InputIt data_global, int count,
T identity, Op op, T* reduction_global) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
typedef CTAReduce<NT, Op> R;
union Shared {
typename R::Storage reduceStorage;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = NV * block;
int count2 = min(NV, count - gid);
// Load a full tile into register in strided order. Set out-of-range values
// with identity.
T data[VT];
DeviceGlobalToRegDefault<NT, VT>(count2, data_global + gid, tid, data,
identity);
// Sum elements within each thread.
T x;
#pragma unroll
for(int i = 0; i < VT; ++i)
x = i ? op(x, data[i]) : data[i];
// Sum thread-totals over the CTA.
x = R::Reduce(tid, x, shared.reduceStorage, op);
// Store the tile's reduction to global memory.
if(!tid)
reduction_global[block] = x;
}
This project aims for simplicity, especially in the simplest and earliest algorithms. The implementations of reduce and scan have been heavily revised and simplified from the original version. Each CTA loads one tile of data and emits the reduction of that data. The host function is called recursively until all values have been folded into a single output.
Most MGPU kernels have special logic to deal with the partial tile at the end of each grid. For reduce and scan, however, we opt to simplify the kernel implementation by taking an init value as an argument. DeviceGlobalToRegDefault loads a full tile of data in strided order; out-of-range values are filled with init, which is chosen to be a neutral value when combined with the the reduction operator op. (Examples are 0 for operator + and 1 for operator *.) Although an identity is not necessary for reduction (it's a minor convenience here), it is necessary for exclusive-scan, and a major convenience for segmented reduction.
After loading a tile of data, each thread folds its VT values into a scalar. Note that adjacent values in the input are not folded together in order; we require the operator be commutative. (i.e. a * b = b * a.) Inputs may be transposed and folded in thread order to support non-commutative operators, although we feel this is rarely, if ever, necessary in practice.
After each thread has reduced its values into x, the cooperative device subroutine CTAReduce::Reduce folds values across threads into a tile reduction. The first thread in each CTA stores the reduction to global memory.
template<typename InputIt, typename T, typename Op>
MGPU_HOST void Reduce(InputIt data_global, int count, T identity, Op op,
T* reduce_global, T* reduce_host, CudaContext& context) {
MGPU_MEM(T) totalDevice;
if(!reduce_global) {
totalDevice = context.Malloc<T>(1);
reduce_global = totalDevice->get();
}
if(count <= 256) {
typedef LaunchBoxVT<256, 1> Tuning;
KernelReduce<Tuning><<<1, 256, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global);
MGPU_SYNC_CHECK("KernelReduce");
} else if(count <= 768) {
typedef LaunchBoxVT<256, 3> Tuning;
KernelReduce<Tuning><<<1, 256, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global);
MGPU_SYNC_CHECK("KernelReduce");
} else if(count <= 512 * ((sizeof(T) > 4) ? 4 : 8)) {
typedef LaunchBoxVT<512, ((sizeof(T) > 4) ? 4 : 8)> Tuning;
KernelReduce<Tuning><<<1, 512, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global);
MGPU_SYNC_CHECK("KernelReduce");
} else {
// Launch a grid and reduce tiles to temporary storage.
typedef LaunchBoxVT<256, (sizeof(T) > 4) ? 8 : 16> Tuning;
int2 launch = Tuning::GetLaunchParams(context);
int NV = launch.x * launch.y;
int numBlocks = MGPU_DIV_UP(count, NV);
MGPU_MEM(T) reduceDevice = context.Malloc<T>(numBlocks);
KernelReduce<Tuning><<<numBlocks, launch.x, 0, context.Stream()>>>(
data_global, count, identity, op, reduceDevice->get());
MGPU_SYNC_CHECK("KernelReduce");
Reduce(reduceDevice->get(), numBlocks, identity, op, reduce_global,
(T*)0, context);
}
if(reduce_host)
copyDtoH(reduce_host, reduce_global, 1);
}The Reduce host function is invoked recursively until all inputs fit in a single tile. It returns the reduction in device memory, host memory, or both. Inputs of 256 or fewer elements are processed by a single tile with 256 threads and a grain-size of 1. Inputs of 768 or fewer elements are processed by a single tile with a grain-size of 3. Larger inputs are processed by larger tiles, which register block to increase sequential work per thread and amortize the work-inefficient cooperative CTA reduction.
If multiple CTAs are launched, the tile reductions are stored to the temporary array reduceDevice, which is fed back into the host Reduce function. This recursive definition realizes high performance without having to involve "persistent CTAs," a pattern in which a fixed number of CTAs are launched which progressively loop through inputs. Persistant CTAs require occupancy calculation and device knowledge to launch an optimal grid sizes, as well as a fudge factor in the form of oversubscription to smooth out variability in CTA times. Sizing grids to data sizes rather than the number of device SMs keeps code simple: each CTA processes one tile and then exits; the hardware grid scheduler is responsible for load balancing.
template<int NT, typename Op = mgpu::plus<int> >
struct CTAScan {
typedef typename Op::result_type T;
enum { Size = NT, Capacity = 2 * NT + 1 };
struct Storage { T shared[Capacity]; };
MGPU_DEVICE static T Scan(int tid, T x, Storage& storage, T* total,
MgpuScanType type = MgpuScanTypeExc, T identity = (T)0, Op op = Op()) {
storage.shared[tid] = x;
int first = 0;
__syncthreads();
#pragma unroll
for(int offset = 1; offset < NT; offset += offset) {
if(tid >= offset)
x = op(storage.shared[first + tid - offset], x);
first = NT - first;
storage.shared[first + tid] = x;
__syncthreads();
}
*total = storage.shared[first + NT - 1];
if(MgpuScanTypeExc == type)
x = tid ? storage.shared[first + tid - 1] : identity;
__syncthreads();
return x;
}
MGPU_DEVICE static T Scan(int tid, T x, Storage& storage) {
T total;
return Scan(tid, x, storage, &total, MgpuScanTypeExc, (T)0, Op());
}
};CTAScan is a basic implementation that uses double buffering to reduce synhronization. The inclusive scan is computed by ping-ponging data between the left and right halves of the storage buffer each round. If the exclusive scan was requested, each thread returns the preceding thread's inclusive scan value; the first thread returns identity.
////////////////////////////////////////////////////////////////////////////////
// Special partial specialization for CTAScan<NT, ScanOpAdd> on Kepler.
// This uses the shfl intrinsic to reduce scan latency.
#if __CUDA_ARCH__ >= 300
template<int NT>
struct CTAScan<NT, mgpu::plus<int> > {
typedef mgpu::plus<int> Op;
enum { Size = NT, NumSegments = WARP_SIZE, SegSize = NT / NumSegments };
enum { Capacity = NumSegments + 1 };
struct Storage { int shared[Capacity + 1]; };
MGPU_DEVICE static int Scan(int tid, int x, Storage& storage, int* total,
MgpuScanType type = MgpuScanTypeExc, int identity = 0, Op op = Op()) {
// Define WARP_SIZE segments that are NT / WARP_SIZE large.
// Each warp makes log(SegSize) shfl_add calls.
// The spine makes log(WARP_SIZE) shfl_add calls.
int lane = (SegSize - 1) & tid;
int segment = tid / SegSize;
// Scan each segment using shfl_add.
int scan = x;
#pragma unroll
for(int offset = 1; offset < SegSize; offset *= 2)
scan = shfl_add(scan, offset, SegSize);
// Store the reduction (last element) of each segment into storage.
if(SegSize - 1 == lane) storage.shared[segment] = scan;
__syncthreads();
// Warp 0 does a full shfl warp scan on the partials. The total is
// stored to shared[NumSegments]. (NumSegments = WARP_SIZE)
if(tid < NumSegments) {
int y = storage.shared[tid];
int scan = y;
#pragma unroll
for(int offset = 1; offset < NumSegments; offset *= 2)
scan = shfl_add(scan, offset, NumSegments);
storage.shared[tid] = scan - y;
if(NumSegments - 1 == tid) storage.shared[NumSegments] = scan;
}
__syncthreads();
// Add the scanned partials back in and convert to exclusive scan.
scan += storage.shared[segment];
if(MgpuScanTypeExc == type) {
scan -= x;
if(identity && !tid) scan = identity;
}
*total = storage.shared[NumSegments];
__syncthreads();
return scan;
}
MGPU_DEVICE static int Scan(int tid, int x, Storage& storage) {
int total;
return Scan(tid, x, storage, &total, MgpuScanTypeExc, 0);
}
};
#endif // __CUDA_ARCH__ >= 300The CTA shuffle scan implementation takes the form of warp-synchronous programming but without the need for volatile memory qualifiers. We choose to divide the input into 32 equal segments. For 256 threads, we have a segment size of eight, and this is scanned in three calls to shfl_add. The last thread in each segment stores the partial sum to shared memory. After a barrier the partials are warp-scanned with five invocations of shfl_add.
The choice to scan small segments in the upsweep (8 threads/segment) and scan large segments in the spane (32 threads/segment) has significant consequence for work efficiency: in the 256-thread example, each of the eight warps makes three calls to shfl_add in the upsweep, and the spine warp makes five calls, for 29 shuffles in all. By contrast, setting the segment size to 32 performs a five-pass warp scan in the upsweep and a three-pass scan over the eight partials in the spine, calling shfl_add 43 times. Changing the fan-out of scan networks can have implications for both the latency and efficiency.
template<MgpuScanType Type, typename DataIt, typename T, typename Op,
typename DestIt>
MGPU_HOST void Scan(DataIt data_global, int count, T identity, Op op,
T* reduce_global, T* reduce_host, DestIt dest_global,
CudaContext& context) {
MGPU_MEM(T) totalDevice;
if(reduce_host && !reduce_global) {
totalDevice = context.Malloc<T>(1);
reduce_global = totalDevice->get();
}
if(count <= 256) {
typedef LaunchBoxVT<256, 1> Tuning;
KernelScanParallel<Tuning, Type><<<1, 256, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global, dest_global);
MGPU_SYNC_CHECK("KernelScanParallel");
} else if(count <= 768) {
typedef LaunchBoxVT<256, 3> Tuning;
KernelScanParallel<Tuning, Type><<<1, 256, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global, dest_global);
MGPU_SYNC_CHECK("KernelScanParallel");
} else if (count <= 512 * 5) {
typedef LaunchBoxVT<512, 5> Tuning;
KernelScanParallel<Tuning, Type><<<1, 512, 0, context.Stream()>>>(
data_global, count, identity, op, reduce_global, dest_global);
MGPU_SYNC_CHECK("KernelScanParallel");
} else {
typedef LaunchBoxVT<
128, (sizeof(T) > 4) ? 7 : 15, 0,
128, 7, 0,
128, 7, 0
> Tuning;
int2 launch = Tuning::GetLaunchParams(context);
int NV = launch.x * launch.y;
int numBlocks = MGPU_DIV_UP(count, NV);
MGPU_MEM(T) reduceDevice = context.Malloc<T>(numBlocks + 1);
// Reduce tiles into reduceDevice.
KernelReduce<Tuning><<<numBlocks, launch.x, 0, context.Stream()>>>(
data_global, count, identity, op, reduceDevice->get());
MGPU_SYNC_CHECK("KernelReduce");
// Recurse to scan the reductions.
Scan<MgpuScanTypeExc>(reduceDevice->get(), numBlocks, identity, op,
reduce_global, (T*)0, reduceDevice->get(), context);
// Add scanned reductions back into output and scan.
KernelScanDownsweep<Tuning, Type>
<<<numBlocks, launch.x, 0, context.Stream()>>>(data_global, count,
reduceDevice->get(), identity, op, dest_global);
MGPU_SYNC_CHECK("KernelScanDownsweep");
}
if(reduce_host)
copyDtoH(reduce_host, reduce_global, 1);
}
The MGPU Scan implementation executes a reduction in its upsweep to compute carry-in for downsweep scan. We reuse KernelReduce to compute per-tile reductions. The tile reductions are then recursively fed back into the Scan host function. On return, KernelScanDownsweep loads complete tiles from the input, scans them locally, and adds-in the scanned upsweep reductions as carry-in.
Launching kernels on very small inputs doesn't do much work but may still contribute a lot of latency to the pipeline, because the entire queue will wait for a single CTA to finish. We implement a simple intra-tile scan that runs on a singcle CTA and size the launch for shallow and wide kernels, based on input size, to minimize latency. This is the spine scan of our upsweep-spine-downsweep pattern.