
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
A frequently occurring pattern in parallel computing is segmented reduction—a parallel reduction over many irregular-length segments. MGPU provides a common back-end class for evaluating segmented reductions along with three front-end examples for solving real-world problems: segmented reduction on CSR-style segment descriptors, a thrust-style reduce-by-key, and a CSR sparse matrix * vector operator (Spmv).

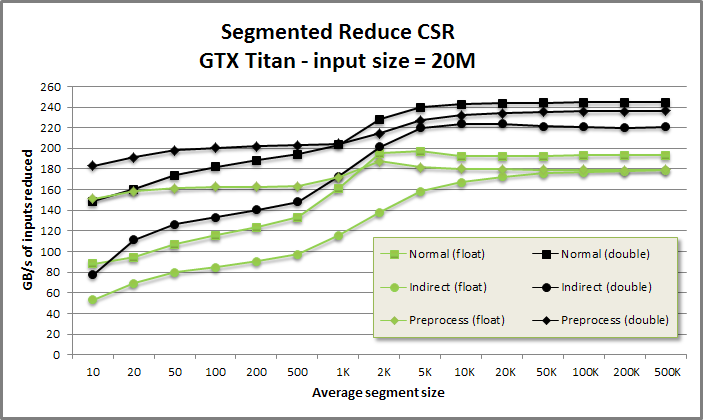
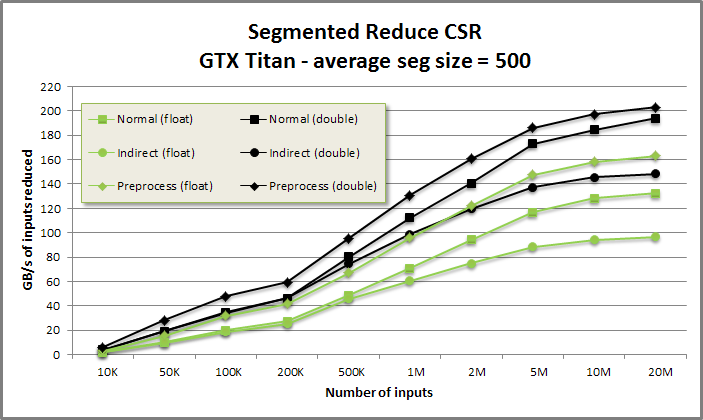
Segmented reduce benchmark from benchmarksegreduce/benchmarksegreduce.cu
Segmented reduce demonstration from demo/demo.cu
void DemoSegReduceCsr(CudaContext& context) {
printf("\n\nSEGMENTED REDUCE-CSR DEMONSTRATION\n\n");
int count = 100;
const int SegmentStarts[] = {
0, 9, 19, 25, 71, 87, 97
};
const int NumSegments = sizeof(SegmentStarts) / sizeof(int);
MGPU_MEM(int) csrDevice = context.Malloc(SegmentStarts, NumSegments);
MGPU_MEM(int) valsDevice = context.GenRandom<int>(count, 1, 5);
printf("Segment starts (CSR):\n");
PrintArray(*csrDevice, "%4d", 10);
printf("\nValues:\n");
PrintArray(*valsDevice, "%4d", 10);
MGPU_MEM(int) resultsDevice = context.Malloc<int>(NumSegments);
SegReduceCsr(valsDevice->get(), csrDevice->get(), count, NumSegments,
false, resultsDevice->get(), (int)0, mgpu::plus<int>(), context);
printf("\nReduced values:\n");
PrintArray(*resultsDevice, "%4d", 10);
}
SEGMENTED REDUCE-CSR DEMONSTRATION
Segment starts (CSR):
0: 0 9 19 25 71 87 97
Values:
0: 1 5 5 1 2 5 1 1 4 4
10: 5 3 4 4 4 2 2 4 2 5
20: 5 1 5 1 4 5 1 4 2 2
30: 2 3 3 1 4 2 4 2 1 2
40: 5 1 2 2 3 1 2 5 4 1
50: 2 5 4 2 4 1 3 2 4 4
60: 4 4 4 3 4 4 1 5 1 1
70: 3 2 3 1 4 1 1 4 4 4
80: 3 5 5 3 2 1 5 5 4 5
90: 4 2 2 3 5 5 1 4 1 5
Reduced values:
0: 25 34 21 129 48 36 10// SegReducePreprocessData is defined in segreduce.cuh. It includes: // - limits for CSR->tiles // - packed thread codes for each thread in the reduction // - (optional) CSR2 array of filtered segment offsets struct SegReducePreprocessData; // SegReduceCsr runs a segmented reduction given an input and a sorted list of // segment start offsets. This implementation requires operators support // commutative (a + b = b + a) and associative (a + (b + c) = (a + b) + c) // evaluation. // In the segmented reduction, reduce-by-key, and Spmv documentation, "segment" // and "row" are used interchangably. A // // InputIt data_global - Data value input. // int count - Size of input array data_global. // CsrIt csr_global - List of integers for start of each segment. // The first entry must be 0 (indicating that the // first segment starts at offset 0). // Equivalent to exc-scan of segment sizes. // If supportEmpty is false: must be ascending. // If supportEmpty is true: must be non-descending. // int numSegments - Size of segment list csr_global. Must be >= 1. // bool supportEmpty - Basic seg-reduce code does not support empty // segments. // Set supportEmpty = true to add pre- and post- // processing to support empty segments. // OutputIt dest_global - Output array for segmented reduction. Allocate // numSegments elements. Should be same data type as // InputIt and identity. // T identity - Identity for reduction operation. Eg, use 0 for // addition or 1 for multiplication. // Op op - Reduction operator. Model on std::plus<>. MGPU // provides operators mgpu::plus<>, minus<>, // multiplies<>, modulus<>, bit_or<> bit_and<>, // bit_xor<>, maximum<>, and minimum<>. // CudaContext& context - MGPU context support object. All kernels are // launched on the associated stream. template<typename InputIt, typename CsrIt, typename OutputIt, typename T, typename Op> MGPU_HOST void SegReduceCsr(InputIt data_global, int count, CsrIt csr_global, int numSegments, bool supportEmpty, OutputIt dest_global, T identity, Op op, CudaContext& context); // IndirectReduceCsr is like SegReduceCsr but with one level of source // indirection. The start of each segment/row i in data_global starts at // sources_global[i]. // SourcesIt sources_global - List of integers for source data of each segment. // Must be numSegments in size. template<typename InputIt, typename CsrIt, typename SourcesIt, typename OutputIt, typename T, typename Op> MGPU_HOST void IndirectReduceCsr(InputIt data_global, int count, CsrIt csr_global, SourcesIt sources_global, int numSegments, bool supportEmpty, OutputIt dest_global, T identity, Op op, CudaContext& context); // SegReduceCsrPreprocess accelerates multiple seg-reduce calls on different // data with the same segment geometry. Partitioning and CSR->CSR2 transform is // off-loaded to a preprocessing pass. The actual reduction is evaluated by // SegReduceApply. template<typename T, typename CsrIt> MGPU_HOST void SegReduceCsrPreprocess(int count, CsrIt csr_global, int numSegments, bool supportEmpty, std::auto_ptr<SegReducePreprocessData>* ppData, CudaContext& context); template<typename InputIt, typename DestIt, typename T, typename Op> MGPU_HOST void SegReduceApply(const SegReducePreprocessData& preprocess, InputIt data_global, T identity, Op op, DestIt dest_global, CudaContext& context);
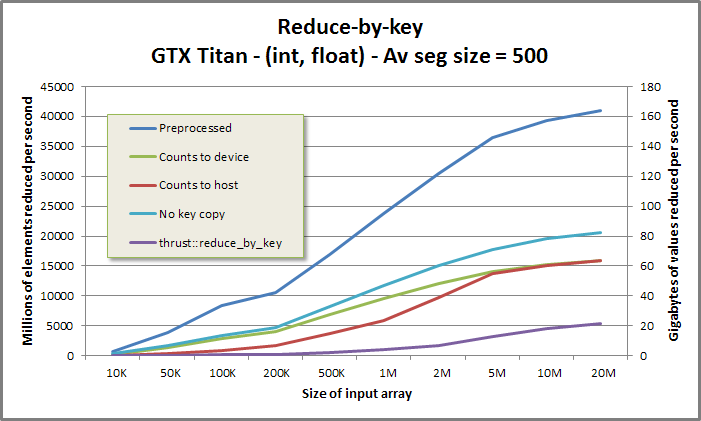
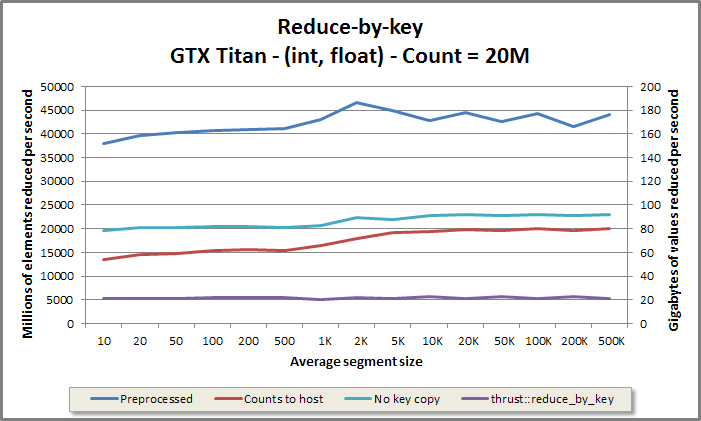
Reduce-by-key benchmark from benchmarkreducebykey/benchmarkreducebykey.cu
Segmented reduce demonstration from demo/demo.cu
void DemoReduceByKey(CudaContext& context) {
printf("\n\nREDUCE BY KEY DEMONSTRATION\n\n");
int count = 100;
std::vector<int> keys(count);
for(int i = 1; i < count; ++i)
keys[i] = keys[i - 1] + (0 == Rand(0, 9));
MGPU_MEM(int) keysDevice = context.Malloc(keys);
MGPU_MEM(int) valsDevice = context.GenRandom<int>(count, 1, 5);
printf("Keys:\n");
PrintArray(*keysDevice, "%4d", 10);
printf("\nValues:\n");
PrintArray(*valsDevice, "%4d", 10);
MGPU_MEM(int) keysDestDevice = context.Malloc<int>(count);
MGPU_MEM(int) destDevice = context.Malloc<int>(count);
int numSegments;
ReduceByKey(keysDevice->get(), valsDevice->get(), count,
0, mgpu::plus<int>(), mgpu::equal_to<int>(), destDevice->get(),
keysDestDevice->get(), &numSegments, (int*)0, context);
printf("\nReduced keys:\n");
PrintArray(*keysDestDevice, numSegments, "%4d", 10);
printf("\nReduced values:\n");
PrintArray(*destDevice, numSegments, "%4d", 10);
}REDUCE BY KEY DEMONSTRATION
Keys:
0: 0 0 0 1 1 1 2 2 2 2
10: 2 2 2 2 2 2 2 2 2 2
20: 2 2 2 2 2 2 2 2 2 2
30: 2 2 2 2 2 3 3 3 3 3
40: 3 3 3 4 4 5 5 5 5 5
50: 5 5 5 5 5 5 6 6 6 6
60: 6 6 6 6 6 6 6 6 6 7
70: 8 8 8 8 8 8 8 8 8 8
80: 8 8 8 8 8 8 8 8 8 8
90: 8 8 8 8 8 8 8 8 8 8
Values:
0: 2 4 2 4 1 5 3 2 4 4
10: 2 5 2 2 5 3 3 5 3 3
20: 2 2 1 4 4 2 1 4 1 3
30: 1 3 2 4 2 5 1 2 1 5
40: 4 4 1 5 4 1 5 2 3 4
50: 1 2 4 2 5 4 3 4 5 3
60: 3 4 2 1 1 2 3 3 2 2
70: 2 4 1 5 5 2 2 4 3 1
80: 3 5 4 1 2 3 2 2 5 5
90: 1 3 3 3 4 5 5 2 4 3
Reduced keys:
0: 0 1 2 3 4 5 6 7 8
Reduced values:
0: 8 10 82 23 9 33 36 2 94//////////////////////////////////////////////////////////////////////////////// // kernels/reducebykey.csr typedef SegReducePreprocessData ReduceByKeyPreprocessData; // ReduceByKey runs a segmented reduction given a data input and a matching set // of keys. This implementation requires operators support commutative // (a + b = b + a) and associative (a + (b + c) = (a + b) + c) evaluation. // It roughly matches the behavior of thrust::reduce_by_key. // KeysIt keys_global - Key identifier for the segment. // InputIt data_global - Data value input. // int count - Size of input arrays keys_global and // data_global. // ValType identity - Identity for reduction operation. Eg, use 0 for // addition or 1 for multiplication. // Op op - Reduction operator. Model on std::plus<>. MGPU // provides operators mgpu::plus<>, minus<>, // multiplies<>, modulus<>, bit_or<> bit_and<>, // bit_xor<>, maximum<>, and minimum<>. // Comp comp - Operator for comparing adjacent adjacent keys. // Must return true if two adjacent keys are in the // same segment. Use mgpu::equal_to<KeyType>() by // default. // KeyType* keysDest_global - If this pointer is not null, return the first // key from each segment. Must be sized to at least // the number of segments. // DestIt dest_global - Holds the reduced data. Must be sized to at least // the number of segments. // int* count_host - The number of segments, returned in host memory. // May be null. // int* count_global - The number of segments, returned in device memory. // This avoids a D->H synchronization. May be null. // CudaContext& context - MGPU context support object. template<typename KeysIt, typename InputIt, typename DestIt, typename KeyType, typename ValType, typename Op, typename Comp> MGPU_HOST void ReduceByKey(KeysIt keys_global, InputIt data_global, int count, ValType identity, Op op, Comp comp, KeyType* keysDest_global, DestIt dest_global, int* count_host, int* count_global, CudaContext& context); // ReduceByKeyPreprocess accelerates multiple reduce-by-key calls on different // data with the same segment geometry. The actual reduction is evaluated by // ReduceByKeyApply. template<typename ValType, typename KeyType, typename KeysIt, typename Comp> MGPU_HOST void ReduceByKeyPreprocess(int count, KeysIt keys_global, KeyType* keysDest_global, Comp comp, int* count_host, int* count_global, std::auto_ptr<ReduceByKeyPreprocessData>* ppData, CudaContext& context); template<typename InputIt, typename DestIt, typename T, typename Op> MGPU_HOST void ReduceByKeyApply(const ReduceByKeyPreprocessData& preprocess, InputIt data_global, T identity, Op op, DestIt dest_global, CudaContext& context);
Spmv benchmark from benchmarkspmvcsr/benchmarkspmvcsr.cu
Download test matrices here.
//////////////////////////////////////////////////////////////////////////////// // kernels/spmvcsr.cuh typedef SegReducePreprocessData SpmvPreprocessData; // SpmvCsr[Unary|Binary] evaluates the product of a sparse matrix (CSR format) // with a dense vector. // SpmvCsrIndirect[Unary|Binary] uses indirection to lookup the start of each // matrix_global and cols_global on a per-row basis. // Unary methods reduce on the right-hand side vector values. // Binary methods reduce the product of the left-hand side matrix value with the // right-hand side vector values. // MatrixIt matrix_global - Left-hand side data for binary Spmv. There are nz // non-zero matrix elements. These are loaded and // combined with the vector values with mulOp. // ColsIt cols_global - Row identifiers for the right-hand side of the // matrix/value products. If element i is the k'th // non-zero in row j, the product is formed as // matrix_global[i] * vec_global[cols_global[i]] // for direct indexing, or, // m = source_global[j] + k // matrix_global[m] * vec_global[cols_global[m]]. // int nz - Number of non-zeros in LHS matrix. Size of // matrix_global and cols_global. // CsrIt csr_global - List of integers for start of each row. // The first entry must be 0 (indicating that the // first row starts at offset 0). // Equivalent to exc-scan of row sizes. // If supportEmpty is false: must be ascending. // If supportEmpty is true: must be non-descending. // SourcesIt sources_global - An indirection array to source each row's data. // The size of each row i is // size_i = csr_global[i + 1] - csr_global[i]. // The starting offset for both the data and column // identifiers is // offset_i = sources_global[i]. // The direct Spmv methods (i.e. those not taking // a sources_global parameter) can be thought of as // indirect methods with sources_global = csr_global. // int numRows - Size of segment list csr_global. Must be >= 1. // VecIt vec_global - Input array. Size is the width of the matrix. // For unary Spmv, these values are reduced. // For binary Spmv, the products of the matrix and // vector values are reduced. // bool supportEmpty - Basic seg-reduce code does not support empty rows. // Set supportEmpty = true to add pre- and post- // processing to support empty rows. // DestIt dest_global - Output array. Must be numRows in size. // T identity - Identity for reduction operation. Eg, use 0 for // addition or 1 for multiplication. // MulOp mulOp - Reduction operator for combining matrix value with // vector value. Only defined for binary Spmv. // Use mgpu::multiplies<T>() for default behavior. // AddOp addOp - Reduction operator for reducing vector values // (unary Spmv) or matrix-vector products (binary // Spmv). Use mgpu::plus<T>() for default behavior. // CudaContext& context - MGPU context support object. All kernels are // launched on the associated stream. template<typename ColsIt, typename CsrIt, typename VecIt, typename DestIt, typename T, typename AddOp> MGPU_HOST void SpmvCsrUnary(ColsIt cols_global, int nz, CsrIt csr_global, int numRows, VecIt vec_global, bool supportEmpty, DestIt dest_global, T identity, AddOp addOp, CudaContext& context); template<typename MatrixIt, typename ColsIt, typename CsrIt, typename VecIt, typename DestIt, typename T, typename MulOp, typename AddOp> MGPU_HOST void SpmvCsrBinary(MatrixIt matrix_global, ColsIt cols_global, int nz, CsrIt csr_global, int numRows, VecIt vec_global, bool supportEmpty, DestIt dest_global, T identity, MulOp mulOp, AddOp addOp, CudaContext& context); template<typename ColsIt, typename CsrIt, typename SourcesIt, typename VecIt, typename DestIt, typename T, typename AddOp> MGPU_HOST void SpmvCsrIndirectUnary(ColsIt cols_global, int nz, CsrIt csr_global, SourcesIt sources_global, int numRows, VecIt vec_global, bool supportEmpty, DestIt dest_global, T identity, AddOp addOp, CudaContext& context); template<typename MatrixIt, typename ColsIt, typename CsrIt, typename SourcesIt, typename VecIt, typename DestIt, typename T, typename MulOp, typename AddOp> MGPU_HOST void SpmvCsrIndirectBinary(MatrixIt matrix_global, ColsIt cols_global, int nz, CsrIt csr_global, SourcesIt sources_global, int numRows, VecIt vec_global, bool supportEmpty, DestIt dest_global, T identity, MulOp mulOp, AddOp addOp, CudaContext& context); // SpmvPreprocess[Unary|Binary] accelerates multiple Spmv calls on different // matrix/vector pairs with the same matrix geometry. The actual reduction is // evaluated Spmv[Unary|Binary]Apply. template<typename T, typename CsrIt> MGPU_HOST void SpmvPreprocessUnary(int nz, CsrIt csr_global, int numRows, bool supportEmpty, std::auto_ptr<SpmvPreprocessData>* ppData, CudaContext& context); template<typename T, typename CsrIt> MGPU_HOST void SpmvPreprocessBinary(int nz, CsrIt csr_global, int numRows, bool supportEmpty, std::auto_ptr<SpmvPreprocessData>* ppData, CudaContext& context); template<typename ColsIt, typename VecIt, typename DestIt, typename T, typename MulOp, typename AddOp> MGPU_HOST void SpmvUnaryApply(const SpmvPreprocessData& preprocess, ColsIt cols_global, VecIt vec_global, DestIt dest_global, T identity, AddOp addOp, CudaContext& context); template<typename MatrixIt, typename ColsIt, typename VecIt, typename DestIt, typename T, typename MulOp, typename AddOp> MGPU_HOST void SpmvBinaryApply(const SpmvPreprocessData& preprocess, MatrixIt matrix_global, ColsIt cols_global, VecIt vec_global, DestIt dest_global, T identity, MulOp mulOp, AddOp addOp, CudaContext& context);
The MGPU Segmented Reduction library contains several composable device-code components, such as CTASegReduce and CTASegScan, as well as three optimized reduction front-ends:
Segmented reduction (CSR) - Reduce multiple variable-length segments in parallel. Segment lengths are parameterized in a "compressed sparse row" array, which is the exclusive scan of the array of segment lengths.
Reduce-by-key - Reduce multiple variable-length segments in parallel. Each element is paired with a segment identifier, and segments are defined as all adjacent elements with the same identifier. This front-end is a high-performance alternative to thrust::reduce_by_key.
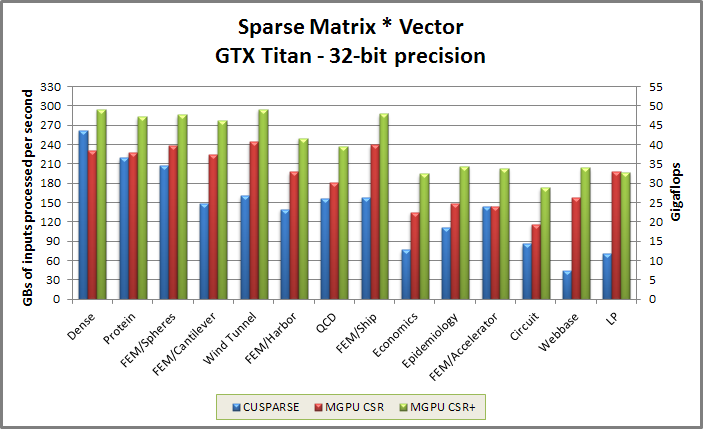
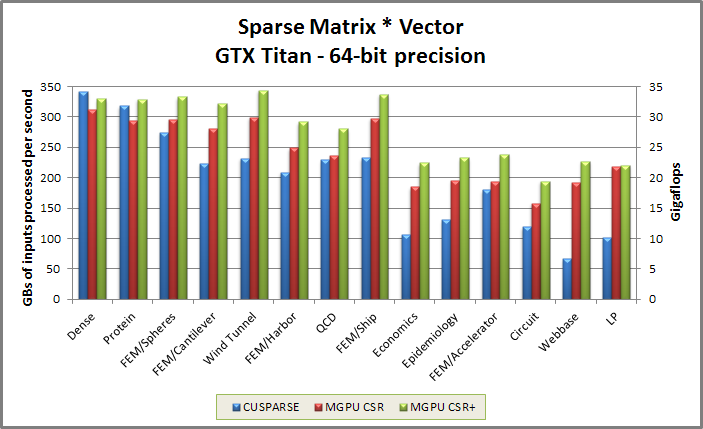
Sparse matrix * vector (CSR) - Multiple a sparse matrix with a dense vector. The matrix is provided as an array of values and column indices, sorted by row. A CSR array defines the matrix geometry.
The front-ends are highly parameterized and support highly-requested features like user-provided reduction operators and indirect sourcing.
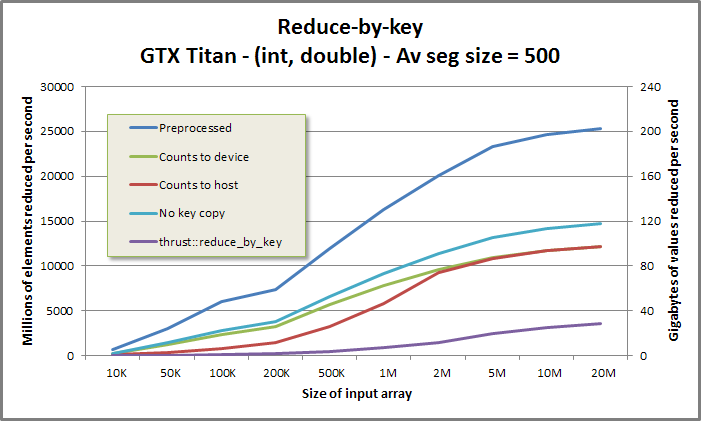
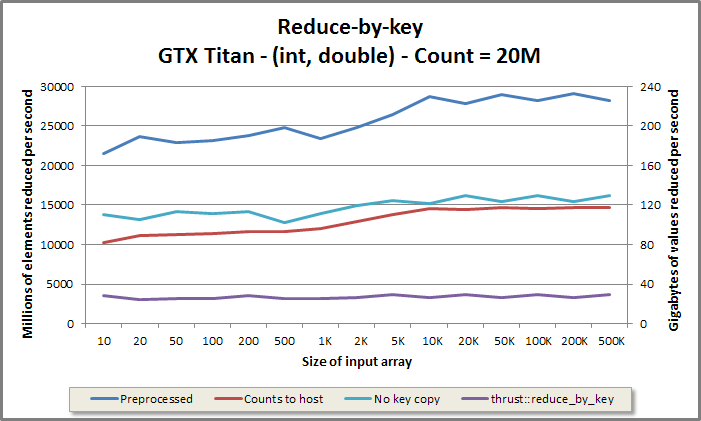
If the user intends to run multiple reductions on different data with the same segment geometry, it is desirable to first preprocess the CSR or segment identifier array into an intermediate data structure, and then to invoke an "apply" function once for each unique set of data. This factors segment discovery out, resulting in a segmented reduction which performs less work. The preprocessed reduce-by-key implementation runs up to twice as fast as the vanilla reduce-by-key; the CSR front-ends see performance boosts of 10-20%.
Many users will be best-served by the provided front-ends, but for those seeking additional flexibility, writing a new front-end is not difficult. Start with the indirect Spmv implementation—the most flexible and customize of the implementations—and add or remove code as needed. Global partitioning, intra-tile reduction, carry-in computation, segment preprocessing, empty segment transformation, and the global spine scan are discrete components which are decoupled from the front-ends; you will likely be able to use these without modification.
The kernels supporting CSR segment descriptors do not directly support empty segments/rows. As discussed in the CSR to COO section, the highest performance is achieved when each segment has at least one element. Rather than adopt a more flexible but slower scheme based on load-balancing search, the library provides a CSR->CSR2 prepass which strips out empty segments. The reduction is performed on re-indexed segments, and a variant of MGPU Bulk Insert is called to copy temporary results into the output buffer and insert zeros for the empty segments. This transformation is opt-in: geometries that have no empty segments by construction avoid the CSR->CSR2 transformation and run at the highest throughputs.
MGPU's implementation of segmented reduction (CSR), reduce-by-key, and Spmv (CSR) have a common core: a load-balanced segmented reduction. For each front-end the kernel reduces all elements in a segment and stores the result to a dense vector.
Consider a set of irregularly-sized segments written as rows:
Segments Values Reductions 0: 5 4 = 9 1: 5 = 5 2: 0 0 4 2 5 = 11 3: 1 3 1 5 1 2 = 13 4: 0 3 0 2 3 4 4 3 = 19 5: 2 5 5 0 5 0 3 4 5 1 1 0 5 3 2 3 3 = 47 6: 3 1 5 4 5 = 18 7: 4 3 3 1 5 = 16 8: 1 4 = 5 9: 5 2 0 0 4 4 2 4 4 2 3 2 3 4 2 0 3 = 44 10: 2 3 5 0 4 0 2 4 2 5 4 0 3 2 = 36 11: 5 4 2 0 = 11 12: 5 3 5 1 0 0 0 3 2 5 = 24 13: 5 5 2 4 0 3 5 = 24 14: 3 0 4 0 5 0 5 5 3 4 5 4 2 4 = 44 15: 4 4 = 8 16: 3 5 1 3 1 5 3 3 5 5 1 = 35 17: 5 0 2 4 2 4 3 2 0 5 0 5 4 5 0 5 2 3 1 = 52 18: 2 2 = 4 19: 2 2 4 0 3 0 3 0 4 1 0 5 = 24
The obvious parallelization is to assign one thread to each row/segment. In Spmv terminology this is the "CSR (scalar)" decomposition. Unfortunately this type of work division creates load imbalance on SIMD processors. Each lane in a warp must wait for the entire warp to finish before returning—threads assigned to long segments effectively stall neighboring threads. For datasets with very large segments, there may not be enough parallelism to properly feed the device's compute units. We can assign warps or entire CTAs to segments, but this is an ad hoc solution and fails when given a diversity of inputs.
Our approach puts load-balancing first: we assign a fixed number of elements to each thread and sequentially accumulate consecutive elements. On encountering the last element in a segment we store the partial reduction for that segment, clear the accumulator, and continue on. After the partial reductions are computed, we cooperatively reduce the carry-out values and add them back into the partial reductions as carry-in values.
Threads Inputs (* = segment end) Partials Carry-out Carry-in 0: 5 4* 5* 0 0 4 2 5* : 9 5 11 => 0* 0 1: 1 3 1 5 1 2* 0 3 : 13 => 3* 0 2: 0 2 3 4 4 3* 2 5 : 16 => 7* 3 3: 5 0 5 0 3 4 5 1 : => 23 7 4: 1 0 5 3 2 3 3* 3 : 17 => 3* 30 5: 1 5 4 5* 4 3 3 1 : 15 => 11* 3 6: 5* 1 4* 5 2 0 0 4 : 5 5 => 11* 11 7: 4 2 4 4 2 3 2 3 : => 24 11 8: 4 2 0 3* 2 3 5 0 : 9 => 10* 35 9: 4 0 2 4 2 5 4 0 : => 21 10 10: 3 2* 5 4 2 0* 5 3 : 5 11 => 8* 31 11: 5 1 0 0 0 3 2 5* : 16 => 0* 8 12: 5 5 2 4 0 3 5* 3 : 24 => 3* 0 13: 0 4 0 5 0 5 5 3 : => 22 3 14: 4 5 4 2 4* 4 4* 3 : 19 8 => 3* 25 15: 5 1 3 1 5 3 3 5 : => 26 3 16: 5 1* 5 0 2 4 2 4 : 6 => 17* 29 17: 3 2 0 5 0 5 4 5 : => 24 17 18: 0 5 2 3 1* 2 2* 2 : 11 4 => 2* 41 19: 2 4 0 3 0 3 0 4 : => 16 2 20: 1 0 5* : 6 => 0* 18 Fixed reductions 9 5 11 13 19 47 18 16 5 44 36 11 24 24 44 8 35 52 4 24
In this figure we've evenly distributed the elements from the 20 segments in the first figure over 21 threads, assigning 8 values per thread (the last thread is assigned a partial number). This choice serves as the grain size, a static tuning parameter for empirically fitting a kernel to a specific generation of microarchitecture. Grain size is abbreviated as VT (values per thread) in the code.
Follow a trip through the VT elements assigned to thread 0:
This is the end of our thread's data, so we return what's left in the accumulator (0) as carry-out.
Without any inter-thread communication we've computed the correct reductions for all segments except the first reduction stored by each thread. To fix-up these partial reductions we run a cooperative segmented-scan on the carry-out values to produce carry-in values, which are added back into the first reduction for each thread.
The fix-up scan requires adding carry-out values from the right-most thread with at least one end flag (a star in the figure) through the carry-out value of the current thread. For example, thread 4 in the figure adds the carry-out values from thread 2 (the right-most starred thread to its left) and thread 3. The sum, 30, is added to its first partial reduction, 17, to produce the final reduction 47.
From a high-level perspective, we process the segmented reduction in tiles with NT threads per CTA and VT values per thread, with NV = NT * VT total elements per tile. Values and segment identifiers are cooperatively loaded and transposed from strided to thread order. Segment/row identifiers are indexed locally, so each thread knows where to store its partial reductions in on-chip memory. Our implementation doesn't directly support empty segments, so the maximum number of reductions per tile is NV, which fits in shared memory.
After locally computing reductions, each CTA emits one carry-out value to an auxiliary array. A special streaming kernel scans carry-out values and redistributes them into the destination reductions (the first reduction for each tile).
This approach exposes parallelism without regard for segment geometry, allowing it to scale over all sorts of problems. The static tuning parameter VT is empirically chosen to maximize throughput for a specific device architecture. This choice is mostly independent of the problem geometry.
The sequential accumulation of consecutive inputs is efficient and easy to implement. The cooperative process of computing carry-in partials for each thread from carry-out partials is not so obvious. We implement the carry-out to carry-in computation as a segmented scan. The user should try to follow the reasoning below, as the intra-CTA segmented scan introduced here (currently only used for segmented reduction) is useful in many other problems.
Consider an array of segment end flags and carry-out partials. We compute the carry-in as the sum of carry-outs for all preceding threads ending in the same segment. Note that a carry-out partial is the sum of values in the segment that begins the subsequent thread. A thread's carry-out is zero if the last element assigned to the thread is also the last element in a segment.
threads : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 end-flags : * * * * seg start : 0 0 0 3 3 3 3 3 3 3 10 11 11 11 11 11 16 16 16 16 16 16 16 16 tid delta : 0 1 2 0 1 2 3 4 5 6 0 0 1 2 3 4 0 1 2 3 4 5 6 7 values : 4 4 3 2 2 5 5 0 5 0 3 4 5 1 1 0 5 3 2 3 3 2 3 1 offset = 1 : 4 8 7 2 4 7 10 5 5 5 3 4 9 6 2 1 5 8 5 5 6 5 5 4 offset = 2 : 4 8 11 2 4 9 14 12 15 10 3 4 9 10 11 7 5 8 10 13 11 10 11 9 offset = 4 : 4 8 11 2 4 9 14 14 19 19 3 4 9 10 11 11 5 8 10 13 16 18 21 22 offset = 8 : 4 8 11 2 4 9 14 14 19 19 3 4 9 10 11 11 5 8 10 13 16 18 21 22 offset = 16 : 4 8 11 2 4 9 14 14 19 19 3 4 9 10 11 11 5 8 10 13 16 18 21 22 carry-in : 0 4 8 11 2 4 9 14 14 19 19 3 4 9 10 11 11 5 8 10 13 16 18 21 carry-out : 22
This example shows 24 threads over five segments. There are four segment ends, that occur inside threads 3, 10, 11, and 17. The last segment is presumed to continue past the end of the tile. Each thread starts by searching for the left-most thread in the tile that will contribute to its carry-in. If thread tid's left-most inputs belong to segment 29, the carry-in value will be the sum of carry-outs from the left-most thread with a carry-out for segment 29 through tid - 1. In this example, the "seg start" line is the index of the left-most thread with a carry-out belonging to the same segment as tid. If a thread contains a segment end, it points to itself; not to its immediate predecessor.
tidDelta is the difference between a thread's index and the index of the left-most thread ending in the same segment. To achieve a segment scan we simply scan level-by-level, adding the value from slot [tid - offset] while tidDelta >= offset. Values that are modified each round are marked in green. Note that tidDelta >= offset for all green values.
This effects an inclusive scan. After all levels have been processed, each thread grabs its predecessor's carry-in scan, which is the exclusive scan. It's this exclusive scan that serves as the carry-in value. Note that the carry-in value is only actually used by threads covering segment ends.
Scan from CTAScan:
#pragma unroll
for(int offset = 1; offset < NT; offset += offset) {
if(tid >= offset)
x = op(storage.shared[first + tid - offset], x);
first = NT - first;
storage.shared[first + tid] = x;
__syncthreads();
}
Segmented scan from CTASegScan:
#pragma unroll
for(int offset = 1; offset < NT; offset += offset) {
if(tidDelta >= offset)
x = op(storage.values[first + tid - offset], x);
first = NT - first;
storage.values[first + tid] = x;
__syncthreads();
}
The segmented scan process has the identical logic as a basic, unsegmented scan, except instead of adding when tid >= offset (so that tid - offset is in bounds) we add when tidDelta >= offset (so that tid - offset holds a partial carry-out reduction of the desired segment). If all threads belong to the same segment, tidDelta = tid naturally, and we see the segmented scan flow matching that of the unsegmented scan.
template<int NT>
MGPU_DEVICE int DeviceFindSegScanDelta(int tid, bool flag, int* delta_shared) {
const int NumWarps = NT / 32;
int warp = tid / 32;
int lane = 31 & tid;
uint warpMask = 0xffffffff>> (31 - lane); // inclusive search
uint ctaMask = 0x7fffffff>> (31 - lane); // exclusive search
uint warpBits = __ballot(flag);
delta_shared[warp] = warpBits;
__syncthreads();
if(tid < NumWarps) {
uint ctaBits = __ballot(0 != delta_shared[tid]);
int warpSegment = 31 - clz(ctaMask & ctaBits);
int start = (-1 != warpSegment) ?
(31 - clz(delta_shared[warpSegment]) + 32 * warpSegment) : 0;
delta_shared[NumWarps + tid] = start;
}
__syncthreads();
// Find the closest flag to the left of this thread within the warp.
// Include the flag for this thread.
int start = 31 - clz(warpMask & warpBits);
if(-1 != start) start += ~31 & tid;
else start = delta_shared[NumWarps + warp];
__syncthreads();
return tid - start;
}Computing tidDelta is the last remaining cooperative programming challenge for intra-tile segmented reduction. The Fermi intrinsics __ballot (vote between lanes in a warp—each lane contributes one bit of the result word) and __clz (count leading zeros) allow us to write a very fast, if somewhat opaque, implementation.
Each thread submits to DeviceFindSegScanDelta a flag indicating if it contains a segment end. The flags are collected into warp-wide words and stored in shared memory at delta_shared. The low-rank threads then cooperatively pull out one warp word each, and make yet another bitfield with __ballot: this time each bit is set if there is a segment flag anywhere in the warp.
A lane mask and the __clz intrinsic are used together to find the right-most warp to the left of the current warp that contains a segment flag. The low threads then index into the warp word for warpSegment to find the right-most lane to the left of the current thread that contains a segment flag. The right-most thread index for each warp is returned in delta_shared.
Finally, each thread uses the __clz scan to find the closest thread to its left that contains a segment flag. If none exist in the warp, it uses the warp-wide thread index stored in delta_shared.
Although the structure of this computation is very specific to GPU architecture, and uses a number of NVIDIA-specific intrinsics, it is at least isolated to a small section of code. The remainder of the segmented reduction code is mostly structural, and glues together concepts we've already treated.
We provide a single class that computes intra-tile segmented reductions and stores both the reductions and the tile's carry-out to device memory. It requires values and CTA-local segment indices in thread order. The problem-specific front-ends (for segmented reduction CSR, reduce-by-key, and Spmv CSR) are responsible for loading data and (in the case of the CSR algorithms) flattening CSR to row indices.
include/device/ctasegreduce.cuh
// Core segmented reduction code. Supports fast-path and slow-path for intra-CTA
// segmented reduction. Stores partials to global memory.
// Callers feed CTASegReduce::ReduceToGlobal values in thread order.
template<int NT, int VT, bool HalfCapacity, typename T, typename Op>
struct CTASegReduce {
typedef CTASegScan<NT, Op> SegScan;
enum {
NV = NT * VT,
Capacity = HalfCapacity ? (NV / 2) : NV
};
union Storage {
typename SegScan::Storage segScanStorage;
T values[Capacity];
};
template<typename DestIt>
MGPU_DEVICE static void ReduceToGlobal(const int rows[VT + 1], int total,
int tidDelta, int startRow, int block, int tid, T data[VT],
DestIt dest_global, T* carryOut_global, T identity, Op op,
Storage& storage) {
// Run a segmented scan within the thread.
T x, localScan[VT];
#pragma unroll
for(int i = 0; i < VT; ++i) {
x = i ? op(x, data[i]) : data[i];
localScan[i] = x;
if(rows[i] != rows[i + 1]) x = identity;
}
// Run a parallel segmented scan over the carry-out values to compute
// carry-in.
T carryOut;
T carryIn = SegScan::SegScanDelta(tid, tidDelta, x,
storage.segScanStorage, &carryOut, identity, op);
// Store the carry-out for the entire CTA to global memory.
if(!tid) carryOut_global[block] = carryOut;
dest_global += startRow;
if(HalfCapacity && total > Capacity) {
// Add carry-in to each thread-local scan value. Store directly
// to global.
#pragma unroll
for(int i = 0; i < VT; ++i) {
// Add the carry-in to the local scan.
T x2 = op(carryIn, localScan[i]);
// Store on the end flag and clear the carry-in.
if(rows[i] != rows[i + 1]) {
carryIn = identity;
dest_global[rows[i]] = x2;
}
}
} else {
// All partials fit in shared memory. Add carry-in to each thread-
// local scan value.
#pragma unroll
for(int i = 0; i < VT; ++i) {
// Add the carry-in to the local scan.
T x2 = op(carryIn, localScan[i]);
// Store reduction when the segment changes and clear the
// carry-in.
if(rows[i] != rows[i + 1]) {
storage.values[rows[i]] = x2;
carryIn = identity;
}
}
__syncthreads();
// Cooperatively store reductions to global memory.
for(int index = tid; index < total; index += NT)
dest_global[index] = storage.values[index];
__syncthreads();
}
}
};CTASegReduce is sensitive to the resource limits of the GPU. For data types larger than 4 bytes, a space-saving "half capacity" mode is supported. This mode provisions only enough shared memory in the encapsulated Storage type to hold half of the tile's NV values in memory at once. Callers that opt-in to the half-capacity mode typically load data cooperatively, in strided order, and transpose through shared memory in two passes.
Thread-order data and row indices are passed to CTASegReduce::ReduceToGlobal. The function calculates the reduction in three phases:
An upsweep phase sequentially computes the thread-local segmented reduction and passes the carry-out to the spine scan.
T x, localScan[VT];
#pragma unroll
for(int i = 0; i < VT; ++i) {
x = i ? op(x, data[i]) : data[i];
localScan[i] = x;
if(rows[i] != rows[i + 1]) x = identity;
}
x is the accumulator for the thread. It adds the next element, stores the thread-local reduction to localScan, and is reset to the identity on a segment end.
Each thread submits its carry-out value to CTASegScan::SegScanDelta to perform the cooperative segmented scan and retrieve the thread's carry-in. The tile's carry-out value is stored to global memory here.
The downsweep phase adds the carry-in to each of the local scan values. Once a segment end is encountered, the carry-in is cleared to identity. The reductions (last element in each segment) are compacted in shared memory then cooperatively streamed to device memory. If the half-capacity mode is used, all the reductions may not be able to fit in shared memory. In this case, the program branches to a loop that adds the carry-in to local scan values and stores directly to global memory. Note that this slow case is only taken when the average segment length over the tile is less than 2.0, a very unlikely occurrence for common applications.
MGPU's reduce-by-key supports a similar interface to thrust::reduce_by_key. Segment identifiers are explicitly paired with each input, so resolving segment indices for each element is as simple as counting discontinuities in the identifier array. The MGPU implementation uses an intermediate format to separate segment index discovery from the reduction computation. The segment identifier array is traversed once, and discontinuity information is extracted, compressed, and stored to the intermediate structure using one word per thread.
include/kernels/reducebykey.cuh
// Stream through keys and find discontinuities. Compress these into a bitfield
// for each thread in the reduction CTA. Emit a count of discontinuities.
// These are scanned to provide limits.
template<typename Tuning, typename KeysIt, typename Comp>
MGPU_LAUNCH_BOUNDS void KernelReduceByKeyPreprocess(KeysIt keys_global,
int count, int* threadCodes_global, int* counts_global, Comp comp) {
typedef typename std::iterator_traits<KeysIt>::value_type T;
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
union Shared {
T keys[NT * (VT + 1)];
int indices[NT];
typename CTAScan<NT>::Storage scanStorage;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = NV * block;
int count2 = min(NV + 1, count - gid);
// Load the keys for this tile with one following element. This allows us
// to determine end flags for all segments.
DeviceGlobalToShared2<NT, VT, VT + 1>(count2, keys_global + gid, tid,
shared.keys);
// Compare adjacent keys in each thread and mark discontinuities in
// endFlags bits.
int endFlags = 0;
if(count2 > NV) {
T key = shared.keys[VT * tid];
#pragma unroll
for(int i = 0; i < VT; ++i) {
T next = shared.keys[VT * tid + 1 + i];
if(!comp(key, next)) endFlags |= 1<< i;
key = next;
}
} else {
T key = shared.keys[VT * tid];
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = VT * tid + 1 + i;
T next = shared.keys[index];
if(index == count2 || (index < count2 && !comp(key, next)))
endFlags |= 1<< i;
key = next;
}
}
__syncthreads();
// Count the number of encountered end flags.
int total;
int scan = CTAScan<NT>::Scan(tid, popc(endFlags), shared.scanStorage,
&total);
if(!tid)
counts_global[block] = total;
if(total) {
// Find the segmented scan start for this thread.
int tidDelta = DeviceFindSegScanDelta<NT>(tid, 0 != endFlags,
shared.indices);
// threadCodes:
// 12:0 - end flags for up to 13 values per thread.
// 19:13 - tid delta for up to 128 threads.
// 30:20 - tile-local offset for first segment end in thread.
int threadCodes = endFlags | (tidDelta<< 13) | (scan<< 20);
threadCodes_global[NT * block + tid] = threadCodes;
}
}KernelReduceByKeyPreprocess is launched with VT elements assigned to each thread. Segment identifiers (called keys to match thrust's parlance) are cooperatively loaded and transposed to thread order. We load NV + 1 keys per tile (one for each element plus the first key for the next tile) and VT + 1 keys per thread. This lets us establish discontinuity (segment end) for each element.
Segment ends are compressed in the bitfield endFlags. The number of segment ends per thread are exclusive scanned, and the total is stored to counts_global. The tidDelta for each thread is computed with DeviceFindSegScanDelta. The segment end bits, segment offset, and tidDelta are compacted into a single word per thread and stored as an accelerated intermediate structure:
tidDelta for up to 128 threads.After KernelReduceByKey returns, we run a global exclusive scan over the tile segment counts. Combined with the compressed segment words, this is sufficient information for constructing row indices for each element without having to make a second pass through the keys.
In fact, this solution serves as a common preprocessing format for all three of our segmented reduction formats. If the segment geometry is constant but the input values change (as is common with Spmv usage, where the matrix data is fixed but the dense right-hand-side vector changes each iteration), it is desirable to hoist out segment discovery into a preprocessing pass. The kernel that actually computes the segmented reduction now loads only one word per thread (with up to 13 values per thread), and has quick access to segment indices, without having to compute any CSR->COO flattening:
The scanned per-tile segment count array provides the index of the first segment in each tile.
Bits 30:20 of the intermediate format's compressed word provides the tile-local index of the first segment for each thread.
Bits 12:0 of the compressed word provide segment end flags for each value in thread order.
Row indices for each element are quickly synthesized using these terms.
The reduction computation for reduce-by-key not only shares an intermediate format with the preprocessed format for segmented reduction CSR, but shares the kernel and host code as well.
include/kernels/segreducecsr.cuh
template<typename Tuning, typename InputIt, typename DestIt, typename T,
typename Op>
MGPU_LAUNCH_BOUNDS void KernelSegReduceApply(const int* threadCodes_global,
int count, const int* limits_global, InputIt data_global, T identity,
Op op, DestIt dest_global, T* carryOut_global) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
const bool HalfCapacity = (sizeof(T) > sizeof(int)) && Params::HalfCapacity;
const bool LdgTranspose = Params::LdgTranspose;
typedef CTAReduce<NT, Op> FastReduce;
typedef CTASegReduce<NT, VT, HalfCapacity, T, Op> SegReduce;
typedef CTASegReduceLoad<NT, VT, HalfCapacity, LdgTranspose, T>
SegReduceLoad;
union Shared {
int csr[NV];
typename FastReduce::Storage reduceStorage;
typename SegReduce::Storage segReduceStorage;
typename SegReduceLoad::Storage loadStorage;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = NV * block;
int count2 = min(NV, count - gid);
int limit0 = limits_global[block];
int limit1 = limits_global[block + 1];
int threadCodes = threadCodes_global[NT * block + tid];
// Load the data and transpose into thread order.
T data[VT];
SegReduceLoad::LoadDirect(count2, tid, gid, data_global, identity, data,
shared.loadStorage);
// Compute the range.
SegReduceRange range = DeviceShiftRange(limit0, limit1);
if(range.total) {
// Expand the segment indices.
int segs[VT + 1];
DeviceExpandFlagsToRows<VT>(threadCodes>> 20, threadCodes, segs);
// Reduce tile data and store to dest_global. Write tile's carry-out
// term to carryOut_global.
int tidDelta = 0x7f & (threadCodes>> 13);
SegReduce::ReduceToGlobal(segs, range.total, tidDelta, range.begin,
block, tid, data, dest_global, carryOut_global, identity, op,
shared.segReduceStorage);
} else {
// If there are no end flags in this CTA, use a fast reduction.
T x;
#pragma unroll
for(int i = 0; i < VT; ++i)
x = i ? op(x, data[i]) : data[i];
x = FastReduce::Reduce(tid, x, shared.reduceStorage, op);
if(!tid)
carryOut_global[block] = x;
}
}KernelSegReduceApply operates on the compressed thread codes generated by KernelReduceByKeyPreprocess (for reduce-by-key) or KernelBuildCsrPlus (for segmented reduction CSR). Compile-time tuning parameters are marshaled through the launch box mechanism: the caller can request a half-capacity transpose for data types larger than int, and it can request an __ldg load for sm_35 architectures and later to load values directly into thread order without requiring a transpose through shared memory.
The kernel specializes CTASegReduce and unions its storage into the shared memory object. CTASegReduce contains encapsulates the logic of the intra-tile reduction, and is leveraged by all our front-ends.
CTASegReduceLoad encapsulates data-loading logic for segmented reduction CSR. It supports a superset of what reduce-by-key requires, including indirect segment sources. For the preprocessed kernel we support only the basic direct indexing.
The kernel loads limit0 and limit1 from limits_global. For reduce-by-key this array provides the exclusive scan of per-tile segment counts. For segmented reduction CSR it's a compatible definition: the index of the first segment in each tile, with a continuation flag in the most significant bit.
include/device/ctasegreduce.cuh
template<int VT>
MGPU_DEVICE void DeviceExpandFlagsToRows(int first, int endFlags,
int rows[VT + 1]) {
rows[0] = first;
#pragma unroll
for(int i = 0; i < VT; ++i) {
if((1<< i) & endFlags) ++first;
rows[i + 1] = first;
}
}range.total is simply the different of limit1 and limit0, which is the number of partial reductions to store (the number of segments ending in the tile). If there are one or more partials, we call DeviceExpandFlagsToRows to materialize segment indices for each element into register from the compressed thread codes. This uses limit0 as the tile's first segment, the high bits of threadCodes for the thread's first segment within the tile, and the low bits of threadCodes as segment end flags on each element.
CTASegReduce::ReduceToGlobal takes value/segment pairs, computes the reductions, and stores them along with the tile's carry-out to global memory. If there are no segment ends in the tile, we have no reductions to store, and only need to compute the carry-out. In this case, we make a special-case branch and compute the carry-out using the standard tile-wide reduction from CTAReduce. This optimization for large segments explains the uptick in throughput when the average segment size exceeds the tile size (around 1000 elements) in the charts here.
An array of segment start offsets is a convenient and space-efficient encoding of segment geometry. This is equivalent to the exclusive scan of segment sizes, and is the same encoding used in the "Compressed Sparse Row" (CSR) sparse matrix format. For convenience we refer to this segment descriptor array as a CSR array.
Unlike the reduce-by-key parameterization, it is possible to specify empty segments in the CSR format. This presents us with an implementation choice. Consider two methods exist for mapping data in CSR format to tiles:
The load-balancing search evenly distributes input values and segments to tiles. Input values and segments are counted together, so that the total number of input values and segments equals the tile size. This flexible pattern supports any segment geometry, including configurations with many consecutive empty segments. In those cases, all NV entities mapped to the tile may be segment descriptors, with no input values, allowing statically-scheduled code to set each output to the identity.
A map of a uniform amount of inputs, NV values, to each tile. This mapping makes no reference to the segment geometry. A binary search into the CSR array for each tile offset i * NV establishes the segment interval for each tile. The CTA cooperatively loads the interval from the CSR and binary searches at offsets i * VT for the segment interval for each thread. Since we load CSR data into on-chip shared memory for the per-thread binary search, and because on-chip memory is finite, we can only handle NV segments per tile. One way to enforce this limit is to disallow empty segments. Each thread handles exactly VT input values, and each input may be the end of a segment, and every segment end is attached to an input value.
Because it processes a full tile of inputs every time, the second mapping exhibits higher throughput than the load-balancing search solution, at the cost of not supporting empty segments. We choose to implement the segmented reduction using this mapping. To support geometries with empty segments, the caller can opt-in to a CSR->CSR2 transform that filters out empty segments, invokes the high-throughput segmented reduction, and finally inserts zeros for the reduction of empty segments. This is a convenient separation of concerns, and the user doesn't pay the load-balancing search tax when the input data is well-formed.
As with merge and merge-like streaming functions, we use a two-phase decomposition to evaluate the segmented reduction on CSR-encoded segments. During partitioning we use a dynamic binary search to map row geometry into tiles: this is analogous to the Merge Path search in our merge function. The segmented reduction kernel launches, loads disjoint intervals from the CSR array, and uses a sequential procedure to materialize segment indices for each input: this is analogous to the use of SerialMerge in the merge implementation.
Once we have segment indices for each input, the segmented reduction CSR, Spmv CSR, and reduce-by-key functions are all handled by the same intra-CTA backend code.
template<int NT, typename CsrIt>
__global__ void KernelPartitionCsrSegReduce(int nz, int nv, CsrIt csr_global,
int numRows, const int* numRows2, int numPartitions, int* limits_global) {
if(numRows2) numRows = *numRows2;
int gid = NT * blockIdx.x + threadIdx.x;
if(gid < numPartitions) {
int key = min(nv * gid, nz);
int ub;
if(key == nz) ub = numRows;
else {
// Upper-bound search for this partition.
ub = BinarySearch<MgpuBoundsUpper>(csr_global, numRows, key,
mgpu::less<int>()) - 1;
// Check if limit points to matching value.
if(key != csr_global[ub]) ub |= 0x80000000;
}
limits_global[gid] = ub;
}
}
template<typename CsrIt>
MGPU_HOST MGPU_MEM(int) PartitionCsrSegReduce(int count, int nv,
CsrIt csr_global, int numRows, const int* numRows2, int numPartitions,
CudaContext& context) {
// Allocate one int per partition.
MGPU_MEM(int) limitsDevice = context.Malloc<int>(numPartitions);
int numBlocks2 = MGPU_DIV_UP(numPartitions, 64);
KernelPartitionCsrSegReduce<64><<<numBlocks2, 64, 0, context.Stream()>>>(
count, nv, csr_global, numRows, numRows2, numPartitions,
limitsDevice->get());
MGPU_SYNC_CHECK("KernelPartitionCsrSegReduce");
return limitsDevice;
}PartitionCsrSegReduce maps the CSR segment descriptor array into uniform-length tiles. It finds disjoint partitions, assigning the descriptor for segments that span multiple tiles to the last tile in the span. If a segment does not start on a tile boundary, the most-significant bit of the limit is set to indicate that the left tile should read one additional segment offset. The partitioning search finds only the first and last segment indices for each tile; filling out per-element segment indices is reserved for the sequential flattening process in the reduction kernel.
It's worth commenting on the use of upper-bound - 1, a frequently recurring partitioning pattern. Consider a CSR array { 0, 957, 1008, 2000, 2312 } and a tile size of 1000. If we lower-bound search the tile boundaries { 0, 1000, 2000 } we have limits { 0, 2, 3 }, corresponding to segment starts { 0, 1008, 2000 }. Segment 0 (offset 0) is correctly mapped as the first segment in tile 0. Segment 3 (offset 2000) is also correctly mapped as the first segment in tile 1. However, segment 2 (offset 1008) is incorrectly mapped as the first segment in tile 1: it should be segment 1 (offset 957).
Now run a binary-search using upper-bound semantics and subtract one from each index: Searching for { 0, 1000, 2000 } in { 0, 957, 1008, 2000, 2312 } yields limits { 0, 1, 3 }. Now segment 1 (offset 957) is correctly identified as the starting segment for tile 1. The segment indices are returned in limits_global, which is passed to all reduction kernels operating on CSR-parameterized segment descriptors.
include/device/ctasegreduce.cuh
struct SegReduceRange {
int begin;
int end;
int total;
bool flushLast;
};
MGPU_DEVICE SegReduceRange DeviceShiftRange(int limit0, int limit1) {
SegReduceRange range;
range.begin = 0x7fffffff & limit0;
range.end = 0x7fffffff & limit1;
range.total = range.end - range.begin;
range.flushLast = 0 == (0x80000000 & limit1);
range.end += !range.flushLast;
return range;
}After partitioning CSR descriptors into tiles, the seg-reduce-CSR and Spmv CSR kernel load the left and right segment indices for their tile. The left limit is the segment index of the left-most segment in the tile. The right limit is the segment index of the first segment in the next tile. If the most-significant bit of the right limit is set, that tile includes an additional segment which spans the tile boundary and ends in a subsequent tile. In the disjoint partitioning this tile belongs to the right-most tile which includes it. When the right limit's most-significant bit is set, we increment the right limit segment index to include the additional segment.
DeviceShiftRange also returns a flushLast value. This is set if the last segment that starts in the tile (the right segment index) also ends on that tile's right boundary. In this case we do not increment the right limit, but instead set flushLast to force a store of the partial reduction at the end of the tile. We can't simply load in the next segment offset, because one past the last segment descriptor may be out of range (when we're at the last segment).
include/device/ctasegreduce.cuh
struct SegReduceTerms {
int endFlags;
int tidDelta;
};
template<int NT, int VT>
MGPU_DEVICE SegReduceTerms DeviceSegReducePrepare(int* csr_shared, int numRows,
int tid, int gid, bool flushLast, int rows[VT + 1], int rowStarts[VT]) {
// Pass a sentinel (end) to point to the next segment start. If we flush,
// this is the end of this tile. Otherwise it is INT_MAX
int endFlags = DeviceExpandCsrRows<NT, VT>(gid + VT * tid, csr_shared,
numRows, flushLast ? (gid + NT * VT) : INT_MAX, rows, rowStarts);
// Find the distance to to scan to compute carry-in for each thread. Use the
// existance of an end flag anywhere in the thread to determine if carry-out
// values from the left should propagate through to the right.
int tidDelta = DeviceFindSegScanDelta<NT>(tid, rows[0] != rows[VT],
csr_shared);
SegReduceTerms terms = { endFlags, tidDelta };
return terms;
}DeviceSegReducePrepare is a utility function called by all segmented reduction front-ends that require CSR-to-COO flattening. It expands compressed segment descriptors to tile-local segment indices, packs segment discontinuities into end flags (for preprocessing), and returns the tidDelta for cooperative segmented scan.
include/device/ctasegreduce.cuh
template<int NT, int VT>
MGPU_DEVICE int DeviceExpandCsrRows(int tidOffset, int* csr_shared,
int numRows, int end, int rows[VT + 1], int rowStarts[VT]) {
// Each thread binary searches for its starting row.
int row = BinarySearch<MgpuBoundsUpper>(csr_shared, numRows, tidOffset,
mgpu::less<int>()) - 1;
// Each thread starts at row and scans forward, emitting row IDs into
// register. Store the CTA-local row index (starts at 0) to rows and the
// start of the row (globally) to rowStarts.
int curOffset = csr_shared[row];
int nextOffset = (row + 1 < numRows) ? csr_shared[row + 1] : end;
rows[0] = row;
rowStarts[0] = curOffset;
int endFlags = 0;
#pragma unroll
for(int i = 1; i <= VT; ++i) {
// Advance the row cursor when the iterator hits the next row offset.
if(tidOffset + i == nextOffset) {
// Set an end flag when the cursor advances to the next row.
endFlags |= 1<< (i - 1);
// Advance the cursor and load the next row offset.
++row;
curOffset = nextOffset;
nextOffset = (row + 1 < numRows) ? csr_shared[row + 1]; : end
}
rows[i] = row;
if(i < VT) rowStarts[i] = curOffset;
}
__syncthreads();
return endFlags;
}DeviceExpandCsrRows flattens CSR array into per-element tile-local segment indices. Each thread starts by binary searching for its global offset in the CSR array mapped into shared memory: the global offset is NV * blockIdx.x + VT * threadIdx.x. As in the global partitioning function KernelPartitionCsrSegReduce, we use an upper-bound - 1 search.
Once each thread has located the located the tile-local index of the segment for the first element, they march forward element-by-element, comparing the global offset of the element to the next segment offset. Because empty segments are disallowed, we need only make one comparison per loop iteration. If the global offset is equal to the next segment's start offset, we advance to the next segment by incrementing the segment counter and loading the next segment's offset. The segment cursor now correctly identifies the current element's segment.
As with MGPU Merge, the compile-time argument VT serves as a tuning parameter. Increasing the parameter improves algorithmic efficiency by decreasing the number of costly binary searches over the entire input (linear searching for per-element flattening remains O(n)). Decreasing the parameter reduces state-per-thread for supporting more concurrent CTAs per SM, improving occupancy and helping the GPU hide latency.
template<typename Tuning, typename CsrIt>
MGPU_LAUNCH_BOUNDS void KernelBuildCsrPlus(int count, CsrIt csr_global,
const int* limits_global, int* threadCodes_global) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
union Shared {
int csr[NV + 1];
typename CTAScan<NT>::Storage scanStorage;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = NV * block;
int count2 = min(NV, count - gid);
int limit0 = limits_global[block];
int limit1 = limits_global[block + 1];
// Transform the row limits into ranges.
SegReduceRange range = DeviceShiftRange(limit0, limit1);
int numRows = range.end - range.begin;
// Load the Csr interval.
DeviceGlobalToSharedLoop<NT, VT>(numRows, csr_global + range.begin, tid,
shared.csr);
// Flatten Csr->COO and return the segmented scan terms.
int rows[VT + 1], rowStarts[VT];
SegReduceTerms terms = DeviceSegReducePrepare<NT, VT>(shared.csr,
numRows, tid, gid, range.flushLast, rows, rowStarts);
// Combine terms into bit field.
// threadCodes:
// 12:0 - end flags for up to 13 values per thread.
// 19:13 - tid delta for up to 128 threads.
// 30:20 - scan offset for streaming partials.
int threadCodes = terms.endFlags | (terms.tidDelta<< 13) | (rows[0]<< 20);
threadCodes_global[NT * block + tid] = threadCodes;
}KernelBuildCsrPlus constructs the segmented reduction accelerator structure, which we call CSR+, for all front-ends taking CSR-format segment descriptors. Although this kernel makes no direct reference to the value data type or operator, it must generate CSR+ data that is compatible with KernelSegReduceApply and KernelSpmvApply. The host functions that launch the construction kernels require the user to provide the value's data type; the size of this type is required for retrieving the grain size VT used by the corresponding apply kernel. CSR+ is intended as a non-serializable intermediate format, generated specifically for one front-end and one value data type.
include/kernels/segreducecsr.cuh
template<typename Tuning, bool Indirect, typename CsrIt, typename SourcesIt,
typename InputIt, typename DestIt, typename T, typename Op>
MGPU_LAUNCH_BOUNDS void KernelSegReduceCsr(CsrIt csr_global,
SourcesIt sources_global, int count, const int* limits_global,
InputIt data_global, T identity, Op op, DestIt dest_global,
T* carryOut_global) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
const bool HalfCapacity = (sizeof(T) > sizeof(int)) && Params::HalfCapacity;
const bool LdgTranspose = Params::LdgTranspose;
typedef CTAReduce<NT, Op> FastReduce;
typedef CTASegReduce<NT, VT, HalfCapacity, T, Op> SegReduce;
typedef CTASegReduceLoad<NT, VT, HalfCapacity, LdgTranspose, T>
SegReduceLoad;
union Shared {
int csr[NV + 1];
typename FastReduce::Storage reduceStorage;
typename SegReduce::Storage segReduceStorage;
typename SegReduceLoad::Storage loadStorage;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = NV * block;
int count2 = min(NV, count - gid);
int limit0 = limits_global[block];
int limit1 = limits_global[block + 1];
SegReduceRange range;
SegReduceTerms terms;
int segs[VT + 1], segStarts[VT];
T data[VT];
if(Indirect) {
// Indirect load. We need to load the CSR terms before loading any data.
range = DeviceShiftRange(limit0, limit1);
int numSegments = range.end - range.begin;
if(range.total) {
// Load the CSR interval.
DeviceGlobalToSharedLoop<NT, VT>(numSegments,
csr_global + range.begin, tid, shared.csr);
// Compute the segmented scan terms.
terms = DeviceSegReducePrepare<NT, VT>(shared.csr, numSegments,
tid, gid, range.flushLast, segs, segStarts);
// Load tile of data in thread order from segment IDs.
SegReduceLoad::LoadIndirect(count2, tid, gid, numSegments,
range.begin, segs, segStarts, data_global, sources_global,
identity, data, shared.loadStorage);
} else {
SegReduceLoad::LoadIndirectFast(tid, gid, range.begin, csr_global,
data_global, sources_global, data, shared.loadStorage);
}
} else {
// Direct load. It is more efficient to load the full tile before
// dealing with data dependencies.
SegReduceLoad::LoadDirect(count2, tid, gid, data_global, identity,
data, shared.loadStorage);
range = DeviceShiftRange(limit0, limit1);
int numSegments = range.end - range.begin;
if(range.total) {
// Load the CSR interval.
DeviceGlobalToSharedLoop<NT, VT>(numSegments,
csr_global + range.begin, tid, shared.csr);
// Compute the segmented scan terms.
terms = DeviceSegReducePrepare<NT, VT>(shared.csr, numSegments,
tid, gid, range.flushLast, segs, segStarts);
}
}
if(range.total) {
// Reduce tile data and store to dest_global. Write tile's carry-out
// term to carryOut_global.
SegReduce::ReduceToGlobal(segs, range.total, terms.tidDelta,
range.begin, block, tid, data, dest_global, carryOut_global,
identity, op, shared.segReduceStorage);
} else {
T x;
#pragma unroll
for(int i = 0; i < VT; ++i)
x = i ? op(x, data[i]) : data[i];
x = FastReduce::Reduce(tid, x, shared.reduceStorage, op);
if(!tid)
carryOut_global[block] = x;
}
}KernelSegReduceCsr is a heavily parameterized kernel which implements segmented reduction (CSR) for both direct and indirect loads. As with most of the kernels in the MGPU library, segmented reduction is latency-limited: we don't have the on-chip resources to launch enough concurrent threads to fully hide memory latency. Engineering code to maximize outstanding loads from global memory means we get more work in before a data dependency stalls the thread. It's for this reason that KernelSegReduceCsr is arranged in two main branches.
When loading data from the indirect sources array, we need to flatten the CSR data into segment indices for each element, then load source offsets from sources_global and use the offset of each element within each segment to gather data items. We run into a number of data dependencies which sections the loads into a number of non-overlapping phases:
Load limit0 and limit1 from limits_global.
Cooperatively load the CSR descriptors from csr_global, between indices limit0 and limit1. Flatten the CSR encoding into segment indices for each element.
Cooperatively load the segment source offsets from sources_global. This is not overlapped with the CSR load in (2) because we have no space to store the source offsets until after we flatten the CSR descriptors and free up their slots in shared memory.
Compute the offset of each element within its segment and gather values from global.
There's an additional optimization here: if no segment ends are mapped into the tile (so that range.total is 0), we use the special LoadIndirectFast method to load values. Rather than computing segment indices and offsets for each element, the CSR flattening is skipped and threads load values from a single address: sources_global[limit0]. Because a tile-wide reduction rather than segmented reduction is used within the tile, we can load out-of-order and exploit the commutative property of our reduction operator. Addresses are rotated to guarantee cache-line alignment, and we load directly from global into register, avoiding a trip through shared memory or the use of __ldg to transpose from strided to thread order.
We could additional branching to overlap phases (2) and (3) when the number of segments is less than half of the tile size, allowing us to fit both CSR descriptors and segment offsets in shared memory at once. However, too many restructuring optimizations of this kind sacrifice program clarity and should be motivated by performance metrics.
The segmented reduction (CSR) which uses direct source indexing did see measurable throughput gains when reordered in its own branch. The kernel would be more compact and more clear if indirect and direct load code paths only diverged at CTASegReduceLoad::IndirectLoad/DirectLoad rather than diverging and re-ordering CSR loading, CSR flattening, data loading, and intra-tile reduction. But this special direct-load branch allows for real optimizations over the simpler common path:
Load limit0 and limit1 from limits_global. Overlap with value loads. We can do this because the values addresses are a function of the threadIdx and blockIdx; they aren't dependent on segment geometry.
Cooperatively load the CSR descriptors into shared memory. These loads are dependent on limit0 and limit1.
If no segment ends are mapped into the tile, we forego loading phase 2, as CSR descriptors aren't required. But even in this case we transpose the values from strided order to thread order (or use __ldg). The optimization we exploited in the indirect case of loading directly into register in strided order is not possible here, because we must load values prior to examining the limit0 and limit1 variables—a data dependency on the limits prior to the value load would prohibit the overlapping in phase (1) and add more latency into the pipeline.
The structure of KernelSegReduceCsr was guided by process of re-ordering operations, benchmarking, and trying again. There are too many moving parts to write fast code without performance metrics. When developing your own kernels, try to factor independent operations into their own functions to facilitate rapid benchmarking and design.
If any number of segment boundaries map into the tile, we use CTASegReduce::ReduceToGlobal to compute partial reductions and store the tile's carry-out. If there are not segment boundaries in the tile, all elements belong to the same segment. We branch to a special case that computes a thread-local reduction over strided order (so that each thread adds together elements NV * blockIdx + VT * i + tid, where 0 <= i < VT). This special-case considerably accelerates large segments. Throughput for geometries with large average segment lengths is boosted by this special-case reduction, running around 20% faster than problems with geometries with smaller segments.