

© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Bulk Remove and Bulk Insert are high-throughput functions for fine-grained parallel array surgery. Bulk Remove compacts an array by removing all elements specified by index. Bulk Insert merges two arrays in parallel by insertion index. Merge Path partitioning for load balancing is introduced here.

Bulk Remove benchmark from benchmarkinsert/benchmarkinsert.cu
Bulk Remove demonstration from tests/demo.cu
void DemoBulkRemove(CudaContext& context) {
printf("\n\nBULK REMOVE DEMONSTRATION:\n\n");
// Use CudaContext::FillAscending to generate 100 integers between 0 and 99.
int N = 100;
MGPU_MEM(int) data = context.FillAscending<int>(N, 0, 1);
printf("Input array:\n");
PrintArray(*data, "%4d", 10);
// Remove every 3rd element from the exclusive scan. Use
// CudaContext::FillAscending to generate removal indices for every 3rd
// integer between 0 and 99.
int RemoveCount = MGPU_DIV_UP(N, 3);
MGPU_MEM(int) remove = context.FillAscending(RemoveCount, 0, 3);
MGPU_MEM(int) data2 = context.Malloc<int>(N - RemoveCount);
BulkRemove(data->get(), N, remove->get(), RemoveCount, data2->get(),
context);
printf("\nRemoving every 3rd element:\n");
PrintArray(*data2, "%4d", 10);
}BULK REMOVE DEMONSTRATION:
Input array:
0: 0 1 2 3 4 5 6 7 8 9
10: 10 11 12 13 14 15 16 17 18 19
20: 20 21 22 23 24 25 26 27 28 29
30: 30 31 32 33 34 35 36 37 38 39
40: 40 41 42 43 44 45 46 47 48 49
50: 50 51 52 53 54 55 56 57 58 59
60: 60 61 62 63 64 65 66 67 68 69
70: 70 71 72 73 74 75 76 77 78 79
80: 80 81 82 83 84 85 86 87 88 89
90: 90 91 92 93 94 95 96 97 98 99
Removing every 3rd element:
0: 1 2 4 5 7 8 10 11 13 14
10: 16 17 19 20 22 23 25 26 28 29
20: 31 32 34 35 37 38 40 41 43 44
30: 46 47 49 50 52 53 55 56 58 59
40: 61 62 64 65 67 68 70 71 73 74
50: 76 77 79 80 82 83 85 86 88 89
60: 91 92 94 95 97 98
Bulk Insert benchmark from benchmarkinsert/benchmarkinsert.cu
Bulk Insert demonstration from tests/demo.cu
void DemoBulkInsert(CudaContext& context) {
printf("\n\nBULK INSERT DEMONSTRATION:\n\n");
// Use CudaContext::FillAscending to generate 100 integers between 0 and 99.
int N = 100;
MGPU_MEM(int) data = context.FillAscending<int>(N, 0, 1);
printf("Input array:\n");
PrintArray(*data, "%4d", 10);
// Insert new elements before every 5 input starting at index 2.
// Use step_iterator for insertion positions and content.
int InsertCount = MGPU_DIV_UP(N - 2, 5);
MGPU_MEM(int) data2 = context.Malloc<int>(N + InsertCount);
mgpu::step_iterator<int> insertData(1000, 10);
mgpu::step_iterator<int> insertIndices(2, 5);
BulkInsert(insertData, insertIndices, InsertCount, data->get(), N,
data2->get(), context);
printf("\nInserting before every 5th element starting at item 2:\n");
PrintArray(*data2, "%4d", 10);
}BULK INSERT DEMONSTRATION:
Input array:
0: 0 1 2 3 4 5 6 7 8 9
10: 10 11 12 13 14 15 16 17 18 19
20: 20 21 22 23 24 25 26 27 28 29
30: 30 31 32 33 34 35 36 37 38 39
40: 40 41 42 43 44 45 46 47 48 49
50: 50 51 52 53 54 55 56 57 58 59
60: 60 61 62 63 64 65 66 67 68 69
70: 70 71 72 73 74 75 76 77 78 79
80: 80 81 82 83 84 85 86 87 88 89
90: 90 91 92 93 94 95 96 97 98 99
Inserting before every 5th element starting at item 2:
0: 0 1 1000 2 3 4 5 6 1010 7
10: 8 9 10 11 1020 12 13 14 15 16
20: 1030 17 18 19 20 21 1040 22 23 24
30: 25 26 1050 27 28 29 30 31 1060 32
40: 33 34 35 36 1070 37 38 39 40 41
50: 1080 42 43 44 45 46 1090 47 48 49
60: 50 51 1100 52 53 54 55 56 1110 57
70: 58 59 60 61 1120 62 63 64 65 66
80: 1130 67 68 69 70 71 1140 72 73 74
90: 75 76 1150 77 78 79 80 81 1160 82
100: 83 84 85 86 1170 87 88 89 90 91
110: 1180 92 93 94 95 96 1190 97 98 99//////////////////////////////////////////////////////////////////////////////// // kernels/bulkremove.cuh // Compact the elements in source_global by removing elements identified by // indices_global. indices_global must be unique, sorted, and range between 0 // and sourceCount - 1. The number of outputs is sourceCount - indicesCount. // IndicesIt should resolve to an integer type. iterators like step_iterator // are supported. // If sourceCount = 10, indicesCount = 6, and indices = (1, 3, 4, 5, 7, 8), then // dest = A0 A2 A6 A9. (All indices between 0 and sourceCount - 1 except those // in indices_global). template<typename InputIt, typename IndicesIt, typename OutputIt> MGPU_HOST void BulkRemove(InputIt source_global, int sourceCount, IndicesIt indices_global, int indicesCount, OutputIt dest_global, CudaContext& context); //////////////////////////////////////////////////////////////////////////////// // kernels/bulkinsert.cuh // Combine aCount elements in a_global with bCount elements in b_global. // Each element a_global[i] is inserted before position indices_global[i] and // stored to dest_global. The insertion indices are relative to the B array, // not the output. Indices must be sorted but not necessarily unique. // If aCount = 5, bCount = 3, and indices = (1, 1, 2, 3, 3), the output is: // B0 A0 A1 B1 A2 B2 A3 A4. template<typename InputIt1, typename IndicesIt, typename InputIt2, typename OutputIt> MGPU_HOST void BulkInsert(InputIt1 a_global, IndicesIt indices_global, int aCount, InputIt2 b_global, int bCount, OutputIt dest_global, CudaContext& context);
Bulk Remove and Bulk Insert are intermediate forms between functions of the scan idiom and functions of MGPU's two-phase idiom. These functions search over their inputs to establish coarse-grained partitionings. Sorted indices are loaded into CTAs and scatter and scan operations remove or insert items with fine-grained control.
Data:
0: 0 1 2 3 4 5 6 7 8 9
10: 10 11 12 13 14 15 16 17 18 19
20: 20 21 22 23 24 25 26 27 28 29
30: 30 31 32 33 34 35 36 37 38 39
40: 40 41 42 43 44 45 46 47 48 49
50: 50 51 52 53 54 55 56 57 58 59
60: 60 61 62 63 64 65 66 67 68 69
70: 70 71 72 73 74 75 76 77 78 79
80: 80 81 82 83 84 85 86 87 88 89
90: 90 91 92 93 94 95 96 97 98 99
Remove indices:
0: 1 4 5 7 10 14 15 16 18 19
10: 27 29 31 32 33 36 37 39 50 59
20: 60 61 66 78 81 83 85 90 91 96
30: 97 98 99For Bulk Remove, we start with a full tile of values plus the interval of remove indices that map into the tile.
Flags:
0: 1 0 1 1 0 0 1 0 1 1
10: 0 1 1 1 0 0 0 1 0 0
20: 1 1 1 1 1 1 1 0 1 0
30: 1 0 0 0 1 1 0 0 1 0
40: 1 1 1 1 1 1 1 1 1 1
50: 0 1 1 1 1 1 1 1 1 0
60: 0 0 1 1 1 1 0 1 1 1
70: 1 1 1 1 1 1 1 1 0 1
80: 1 0 1 0 1 0 1 1 1 1
90: 0 0 1 1 1 1 0 0 0 0A tile-sized buffer of flags is initialized to 1. Poking in 0 will remove the value at that position. Threads scatter 0s for all elements listed in the remove indices array.
Scan of flags: 0: 0 1 1 2 3 3 3 4 4 5 10: 6 6 7 8 9 9 9 9 10 10 20: 10 11 12 13 14 15 16 17 17 18 30: 18 19 19 19 19 20 21 21 21 22 40: 22 23 24 25 26 27 28 29 30 31 50: 32 32 33 34 35 36 37 38 39 40 60: 40 40 40 41 42 43 44 44 45 46 70: 47 48 49 50 51 52 53 54 55 55 80: 56 57 57 58 58 59 59 60 61 62 90: 63 63 63 64 65 66 67 67 67 67 Reduced data: 0: 0 2 3 6 8 9 11 12 13 17 10: 20 21 22 23 24 25 26 28 30 34 20: 35 38 40 41 42 43 44 45 46 47 30: 48 49 51 52 53 54 55 56 57 58 40: 62 63 64 65 67 68 69 70 71 72 50: 73 74 75 76 77 79 80 82 84 86 60: 87 88 89 92 93 94 95
An exclusive scan is run on the flags. Flags that were 1 prior to the scan reserve one slot for their values; flags that were 0 reserve no space. The scanned offsets in green had set flags. Values at the green locations in the tile scatter their values to shared memory at their corresponding scanned locations. In this example, element 0 is stored to location 0; element 1 is skipped (its flag is 0); element 2 is stored to location 1; etc.
How do we find the interval of removal indices to load into the CTA, and where does each CTA store its Bulk Remove output? By insisting on sorted indices (and no duplicate indices) both questions have simple answers:
Remove indices are partioned with a lower-bound binary search, where the keys are the starting offsets for each tile, i.e., multiplies of the block size.
Destination offsets for each tile are inferred from the the tile's input offset (a multiple of the block size) and the removal index offset from 1. Because Bulk Remove requires indices both sorted and unique, a CTA knows where to stream given only its block ID and the location of the first remove index in its range. If NV = 1000, block 8 that loads removal indices (2113, 2423) streams exactly 690 values (1000 - (2423 - 2113)) starting at output position 5887 (8 * 1000 - 2113).
template<int NT, MgpuBounds Bounds, typename It, typename Comp>
__global__ void KernelBinarySearch(int count, It data_global, int numItems,
int nv, int* partitions_global, int numSearches, Comp comp) {
int gid = NT * blockIdx.x + threadIdx.x;
if(gid < numSearches) {
int p = BinarySearch<Bounds>(data_global, numItems,
min(nv * gid, count), comp);
partitions_global[gid] = p;
}
}
template<MgpuBounds Bounds, typename It1, typename Comp>
MGPU_MEM(int) BinarySearchPartitions(int count, It1 data_global, int numItems,
int nv, Comp comp, CudaContext& context) {
const int NT = 64;
int numBlocks = MGPU_DIV_UP(count, nv);
int numPartitionBlocks = MGPU_DIV_UP(numBlocks + 1, NT);
MGPU_MEM(int) partitionsDevice = context.Malloc<int>(numBlocks + 1);
KernelBinarySearch<NT, Bounds>
<<<numPartitionBlocks, NT, 0, context.Stream()>>>(count, data_global,
numItems, nv, partitionsDevice->get(), numBlocks + 1, comp);
return partitionsDevice;
}Many host functions call BinarySearchPartitions to partition problems before calling the logic kernel. If the CTA size is 1000, this launch finds intervals in the argument array with values between 0 and 999, 1000 and 1999, etc. For BulkRemove it maps the correct remove indices into each tile.
Thrust includes a function remove_if that compacts inputs given a corresponding array of predicates. This interface requires multiple trips through the input: the first trip simply counts the number of elements not to remove. Modern GPU functions usually accept sorted arrays of indices (to remove, to insert, or to mark segment heads) because it eliminates a pass that would otherwise need to run just to calculate output locations and sizes.
include/kernels/bulkremove.cuh
template<typename Tuning, typename InputIt, typename IndicesIt,
typename OutputIt>
MGPU_LAUNCH_BOUNDS void KernelBulkRemove(InputIt source_global, int sourceCount,
IndicesIt indices_global, int indicesCount, const int* p_global,
OutputIt dest_global) {
typedef MGPU_LAUNCH_PARAMS Params;
typedef typename std::iterator_traits<InputIt>::value_type T;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
typedef CTAScan<NT, ScanOpAdd> S;
union Shared {
int indices[NV];
typename S::Storage scan;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int gid = block * NV;
sourceCount = min(NV, sourceCount - gid);
// Search for begin and end iterators of interval to load.
int p0 = p_global[block];
int p1 = p_global[block + 1];
// Set the flags to 1. The default is to copy a value.
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = NT * i + tid;
shared.indices[index] = index < sourceCount;
}
__syncthreads();
// Load the indices into register.
int begin = p0;
int indexCount = p1 - p0;
int indices[VT];
DeviceGlobalToReg<NT, VT>(indexCount, indices_global + p0, tid, indices);
// Set the counter to 0 for each index we've loaded.
#pragma unroll
for(int i = 0; i < VT; ++i)
if(NT * i + tid < indexCount)
shared.indices[indices[i] - gid] = 0;
__syncthreads();
// Run a raking scan over the flags. We count the set flags - this is the
// number of elements to load in per thread.
int x = 0;
#pragma unroll
for(int i = 0; i < VT; ++i)
x += indices[i] = shared.indices[VT * tid + i];
__syncthreads();
// Run a CTA scan and scatter the gather indices to shared memory.
int scan = S::Scan(tid, x, shared.scan);
#pragma unroll
for(int i = 0; i < VT; ++i)
if(indices[i]) shared.indices[scan++] = VT * tid + i;
__syncthreads();
// Load the gather indices into register.
DeviceSharedToReg<NT, VT>(NV, shared.indices, tid, indices);
// Gather the data into register. The number of values to copy is
// sourceCount - indexCount.
source_global += gid;
int count = sourceCount - indexCount;
T values[VT];
DeviceGather<NT, VT>(count, source_global, indices, tid, values, false);
// Store all the valid registers to dest_global.
DeviceRegToGlobal<NT, VT>(count, values, tid, dest_global + gid - p0);
}After partitioning, the host launches KernelBulkRemove. The results of the binary search are loaded into p0 and p1. Flags are initialized to 1 as described, except those for last-tile elements which extend past the end of the input: these are set to 0. DeviceGlobalToReg loads indices (p0, p1) into register. Because the indices are unique, there cannot be more than NV indices in the interval (p0, p1), so we can safely load into register with an unrolled loop. We use the local removal indices (the offset of the start of the tile is subtracted from each removal index) and poke 0s into shared memory.
Each thread loads VT flags starting at VT * tid. These are summed and passed to CTAReduce. Scanned flags with corresponding set indices (the scan of flags in green from three figures above) are compacted by conditionally streaming not to VT * tid but to each thread's count scan. Because we had to load flags in thread order (VT * tid + i) rather than strided order (NT * i + tid), it is more efficient to invert the problem from a scatter to a gather.
Finally, the threads cooperatively load sourceCount - indexCount indices in strided order, gather the values from global memory, and store directly to output at dest_global + gid - p0.
The complementary function requires a bit more sophistication to write. Remove is easy, because the array can only get smaller. Insert is harder because the array may grow arbitrarily large, causing load-balancing problems. If we were to assign a fixed amount of inputs (say, 1000) to BulkInsert as we do with BulkRemove, we may not be able to hold the input indices or the expanded array in the CTA's register or shared memory resources.
The caller may want to insert 1000 or even 1,000,000 elements before the first input. How does the kernel handle thousands of consecutive 0s in the insert indices array? Unlike the remove case, we cannot disallow duplicate insert indices without loss of functionality. If BinarySearchPartition mapped 10,000 insert requests into a single tile, the kernel would have to dynamically loop through these requests to fulfill them within the capacity constraints of the device. This is expressly against our philosophy that the logic code should not handle scheduling - that is the domain of the partioning phase.
The solution is to generalize the partitioning code to search over two inputs simultaneously: we want to balance the source data with the insertion requests. For NV = 1000, loading 712 inputs implies we can load no more than 288 indices. This way both the new and the old values get merged without overflowing the resources available for the block.
Searching on two sorted arrays is fortunately very easy. For each tile index i, we look for splitters Ai and Bi such that Ai + Bi = NV * i. CTA i loads input from the interval (Ai, Ai+1) and insertion indices from the interval (NV * i - Ai, NV * (i + 1) - Ai+1). The total number of loaded items is clearly NV. If we can simply calculate the partitions Ai we'll have solved Bulk Insert.
template<MgpuBounds Bounds, typename It1, typename It2, typename Comp>
MGPU_HOST_DEVICE int MergePath(It1 a, int aCount, It2 b, int bCount, int diag,
Comp comp) {
typedef typename std::iterator_traits<It1>::value_type T;
int begin = max(0, diag - bCount);
int end = min(diag, aCount);
while(begin < end) {
int mid = (begin + end)>> 1;
T aKey = a[mid];
T bKey = b[diag - 1 - mid];
bool pred = (MgpuBoundsUpper == Bounds) ?
comp(aKey, bKey) :
!comp(bKey, aKey);
if(pred) begin = mid + 1;
else end = mid;
}
return begin;
}MergePath is a binary search over two sorted arrays that uses a constraint, diag, to reduce the search to one dimension. The search resembles the basic binary search in that we establish an interval over the array a, and loop while begin < end. The primary difference is that instead of comparing a[mid] to a fixed query, we utilize the constraint and compare to b[diag - 1 - mid].
This routine is sound analytically but makes little intuitive sense. Fortunately a 2012 paper Merge Path - Parallel Merging Made Simple by Saher Odeh, Oded Green, Zahi Mwassi, Oz Shmuli, and Yitzhak Birk, provides a visualization for this search to help understand and apply it in diverse situations.
Further Reading: Read Merge Path - Parallel Merging Made Simple to better understand a partitioning strategy that's employed repeatedly in the MGPU algorithms.
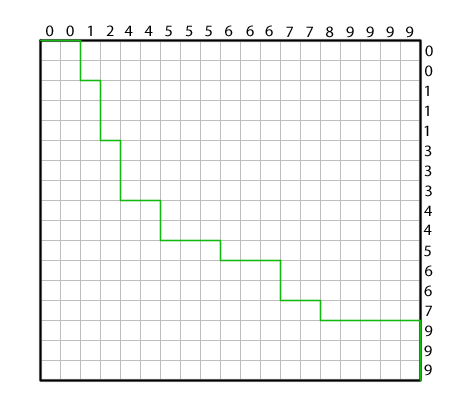
Consider merging the array on the top with the array on the right. Start with the cursor (a pair of pointers to the head of each list) at the upper-left corner. Compare the heads of the lists and advance in the direction of the smaller key; advance to the right if the keys are equal. The curve in green is the Merge Path. It is a visualization of the history of decisions in executing a serial merge.
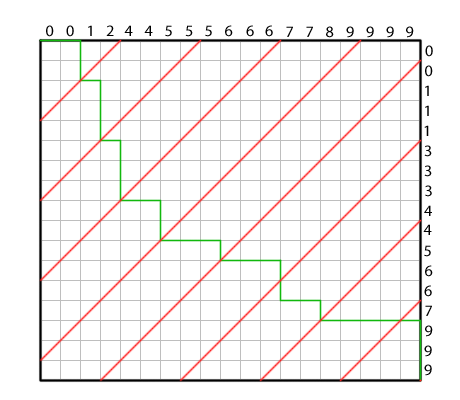
We draw red cross-diagonals over the Merge Path curve. The portion of the path enclosed by consecutive cross-diagonals map the intervals from each source array that contribute to one interval of the merge output. In this example, the first partition is assigned keys 0, 0 from A and 0, 0 from B; the second interval is assigned key 1 from A and keys 1, 1, 1 from B; etc. All partitions are assigned exactly four inputs (and because of the nature of the merge function, four outputs), and each partition can be processed in parallel without communication. If keys in A and B match, the use of use of lower-bound semantics in the MergePath binary search assigns the matching keys in A to the earlier partitions and the matching keys in B to the later partitions, which agrees with the behavior of std::merge.
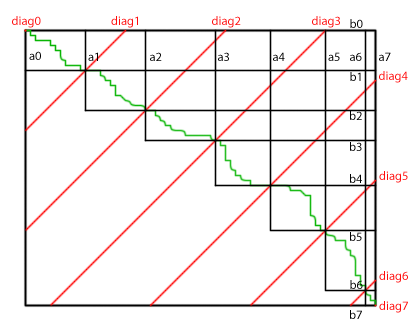
This illustration shows a merge divided into six partitions of equal size plus one partial partition at the lower-right. The eight cross-diagonals (in red) intersect the Merge Path to establish tile partitions (in black). Because the Merge Path can only move down and right (and not diagonal), the length of the curve bounded by two consecutive cross-diagonals is constant and equal to the inter-diagonal spacing. The intersection of the Merge Path projects upwards to define the interval of values in A inside the partition; it projects to the right to define the interval of values in B. The number of steps required for the binary search is the log of the cross-diagonal length.
Important: Merge Path is the history of comparisons made during a sequential merge operation. We want to find the intersection of the Merge Path with regularly-spaced cross-diagonals without actually constructing the Merge Path. We binary search along cross-diagonals, sampling and comparing elements from inputs A and B until we've ascertained where the Merge Path would be, if we had constructed it.
In the CUDA code above, the constraint parameter diag is the distance from the origin that the cross-diagonal intersects the x-axis. Consider tile 3's partition in this figure. A search along cross-diagonal 3 returns the pair (a3, b3), and the search along cross-diagonal 4 returns (a4, b4). Because of the constraint that ai + bi = diag, we need only deal with the coverage interval of A: (a3, a4). When needed, the coverage interval of B is can be computed as (diag3 - a3, diag4 - a4).
How is this applicable to load-balancing Bulk Insert? Consider the array across the top (A) as the sorted list of insertion indices; the array on the right (B) is a counting_iterator<int> representing the positions of the source elements. Bulk Insert is essentially a merge operation where the keys of A are the insertion indices and the keys of B are the natural numbers. Computing the intersection of the Merge Path curve with the cross-diagonal using a constrained binary search solves Bulk Insert's partioning needs.
After mapping a source and insert elements into each tile we can run the actual Bulk Insert logic. This is a scan-oriented kernel and follows the patterns of Bulk Remove.
Insert indices:
0: 1 12 13 14 14 18 20 38 39 44
10: 45 50 50 50 54 56 59 63 68 69
20: 74 75 84 84 88 111 111 119 121 123
30: 126 127 144 153 157 159 163 169 169 175
40: 178 183 190 194 195 196 196 201 219 219
50: 253 256 259 262 262 266 272 273 278 283
60: 284 291 296 297 302 303 306 306 317 318
70: 318 319 319 320 320 323 326 329 330 334
80: 340 349 352 363 366 367 369 374 381 383
90: 383 384 386 388 388 389 393 398 398 399
Tile size = 100 ACount = 22 BCount = 78
Counters:
0: 0 1 0 0 0 0 0 0 0 0
10: 0 0 0 1 0 1 0 1 1 0
20: 0 0 0 1 0 0 1 0 0 0
30: 0 0 0 0 0 0 0 0 0 0
40: 0 0 0 0 0 1 0 1 0 0
50: 0 0 0 1 0 1 0 0 0 0
60: 0 1 1 1 0 0 0 0 1 0
70: 0 1 0 0 0 1 0 0 0 0
80: 1 0 0 0 0 0 1 0 1 0
90: 0 0 0 0 1 0 1 0 0 0 Our example starts with 400 source elements and 100 insertions. A Merge Path search determines that the first tile of 100 elements (NV = 100) should load 22 from A (the insertion array) and 78 from B (the source array). This should be clear from the figure—the insert indices range from 1 to 75 and the implicit source indices range from 0 to 77. Adjusting the Merge Path either way would invalidate the ordering. For example, setting ACount to 23 and BCount to 77 would attempt an insert at position 84 when only source elements 0 to 76 have been loaded.
We allocate and initialize 100 flags to zero. Ones are poked in for each insert index at the index's location plus its value. That is, indices[0] = 1 sets the flag at location 1 (0 + 1); indices[1] = 12 sets the flag at location 13 (1 + 12); indices[2] = 13 sets the flag at location 15 (2 + 13); and so on. Duplicate insertion indices are admissible, as they won't set flags at the same location, because their ranks are different.
Scan of counters:
0: 0 0 1 1 1 1 1 1 1 1
10: 1 1 1 1 2 2 3 3 4 5
20: 5 5 5 5 6 6 6 7 7 7
30: 7 7 7 7 7 7 7 7 7 7
40: 7 7 7 7 7 7 8 8 9 9
50: 9 9 9 9 10 10 11 11 11 11
60: 11 11 12 13 14 14 14 14 14 15
70: 15 15 16 16 16 16 17 17 17 17
80: 17 18 18 18 18 18 18 19 19 20
90: 20 20 20 20 20 21 21 22 22 22
Gather indices:
0: 22 0 23 24 25 26 27 28 29 30
10: 31 32 33 1 34 2 35 3 4 36
20: 37 38 39 5 40 41 6 42 43 44
30: 45 46 47 48 49 50 51 52 53 54
40: 55 56 57 58 59 7 60 8 61 62
50: 63 64 65 9 66 10 67 68 69 70
60: 71 11 12 13 72 73 74 75 14 76
70: 77 15 78 79 80 16 81 82 83 84
80: 17 85 86 87 88 89 18 90 19 91
90: 92 93 94 95 20 96 21 97 98 99
As with Bulk Remove, an exclusive scan is computed across the flags. If the flag was set (indicating an insertion at this position) then we'll gather at that scan offset. If the flag was cleared we subtract the scan from the output rank and add aCount (the number of inserted vertices). This segregates the gather into two forms: inserted values (in green) are referenced by their ranks; source values (in black) are referenced by their ranks plus the number of inserted values.
The loadstore.cuh function DeviceTransferMergeValues interprets gather indices in this format and performs the data transfer. This mechanism is used by other merge-like functions (merge, mergesort, segmented sort, multisets) to move the values in key/value pair operations.
include/kernels/bulkinsert.cuh
template<typename InputIt1, typename IndicesIt, typename InputIt2,
typename OutputIt>
MGPU_HOST void BulkInsert(InputIt1 a_global, IndicesIt indices_global,
int aCount, InputIt2 b_global, int bCount, OutputIt dest_global,
CudaContext& context) {
const int NT = 128;
const int VT = 7;
typedef LaunchBoxVT<NT, VT> Tuning;
int2 launch = Tuning::GetLaunchParams(context);
const int NV = launch.x * launch.y;
MGPU_MEM(int) partitionsDevice = MergePathPartitions<MgpuBoundsLower>(
indices_global, aCount, mgpu::counting_iterator<int>(0), bCount, NV, 0,
mgpu::less<int>(), context);
int numBlocks = MGPU_DIV_UP(aCount + bCount, NV);
KernelBulkInsert<Tuning><<<numBlocks, launch.x, 0, context.Stream()>>>(
a_global, indices_global, aCount, b_global, bCount,
partitionsDevice->get(), dest_global);
}
The host function creates a LaunchBoxVT type to provide tuning parameters to the kernel. We choose a configuration with 128 threads and 7 values per thread as a default, but users who want performance are encouraged to customize this type for their own architectures, data types, and array sizes.
The call to MergePathPartitions runs a MergePath binary search to assign intervals of insert indices and intervals of source data to each CTA. You can imagine the insert indices written along the top of the Merge Path diagram and the natural numbers (corresponding to the positions of the source data) written along the right. A cross-diagonal every NV elements finds an equal partitioning of insert and source elements for each CTA. The intersections of the cross-diagonals with the Merge Path are stored in partitionsDevice, which is passed to the kernel as mp_global.
include/kernels/bulkinsert.cuh
// Insert the values from a_global into the positions marked by indices_global.
template<typename Tuning, typename InputIt1, typename IndicesIt,
typename InputIt2, typename OutputIt>
MGPU_LAUNCH_BOUNDS void KernelBulkInsert(InputIt1 a_global,
IndicesIt indices_global, int aCount, InputIt2 b_global, int bCount,
const int* mp_global, OutputIt dest_global) {
typedef MGPU_LAUNCH_PARAMS Params;
typedef typename std::iterator_traits<InputIt1>::value_type T;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
typedef CTAScan<NT, ScanOpAdd> S;
union Shared {
int indices[NV];
typename S::Storage scan;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int4 range = ComputeMergeRange(aCount, bCount, block, 0, NV, mp_global);
int a0 = range.x; // A is array of values to insert.
int a1 = range.y;
int b0 = range.z; // B is source array.
int b1 = range.w;
aCount = a1 - a0;
bCount = b1 - b0;
// Initialize the indices to 0.
#pragma unroll
for(int i = 0; i < VT; ++i)
shared.indices[NT * i + tid] = 0;
__syncthreads();
// Load the indices.
int indices[VT];
DeviceGlobalToReg<NT, VT>(aCount, indices_global + a0, tid, indices);
// Set the counters for all the loaded indices. This has the effect of
// pushing the scanned values to the right, causing the B data to be
// inserted to the right of each insertion point.
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = NT * i + tid;
if(index < aCount) shared.indices[index + indices[i] - b0] = 1;
}
__syncthreads();
// Run a raking scan over the indices.
int x = 0;
#pragma unroll
for(int i = 0; i < VT; ++i)
x += indices[i] = shared.indices[VT * tid + i];
__syncthreads();
// Run a CTA scan over the thread totals.
int scan = S::Scan(tid, x, shared.scan);
// Complete the scan to compute merge-style gather indices. Indices between
// in the interval (0, aCount) are from array A (the new values). Indices in
// (aCount, aCount + bCount) are from array B (the sources). This style of
// indexing lets us use DeviceTransferMergeValues to do global memory
// transfers.
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = VT * tid + i;
int gather = indices[i] ? scan++ : aCount + index - scan;
shared.indices[index] = gather;
}
__syncthreads();
DeviceTransferMergeValues<NT, VT>(aCount + bCount, a_global + a0,
b_global + b0, bCount, aCount, shared.indices, tid, dest_global + a0 + b0,
false);
}KernelBulkInsert is a straight-forward implementation of the routine described in the algorithm section. Because this function was written in the two-phase decomposition methodology, the important business of mapping work to CUDA cores has already been performed by the time this kernel is launched. ComputeMergeRange reassembles source intervals from the mp_global array, communicating the partitoining of the previous launch to the work-logic kernel.
Kernels are tuned by increasing VT to amortize per-CTA and per-thread costs, improving work-efficiency. Consequently most programs run underoccupied, especially on Kepler. A nice property of both Bulk Remove and Bulk Insert is that only the 32-bit indices are staged in shared memory. Specializing on 64-bit data-types doesn't decrease occupancy on Kepler, which has sufficient RF capacity to accommodate the larger types. Working on 64-bit types increases the atom of transfer to and from global memory while keeping the cost of compute constant. This results in significantly higher throughput (up to 220 GB/s for Bulk Remove on GTX Titan) on 64-bit types compared to 32-bit types (158 GB/s).