
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Segmented sort and locality sort are high-performance variants of mergesort that operate on non-uniform random data. Segmented sort allows us to sort many variable-length arrays in parallel. A list of head indices provided to define segment intervals. Segmented sort is fast: not only is segmentation supported for negligible cost, the function takes advantage of early-exit opportunities to improve throughput over vanilla mergesort. Locality sort detects regions of approximate sortedness without requiring annotations.
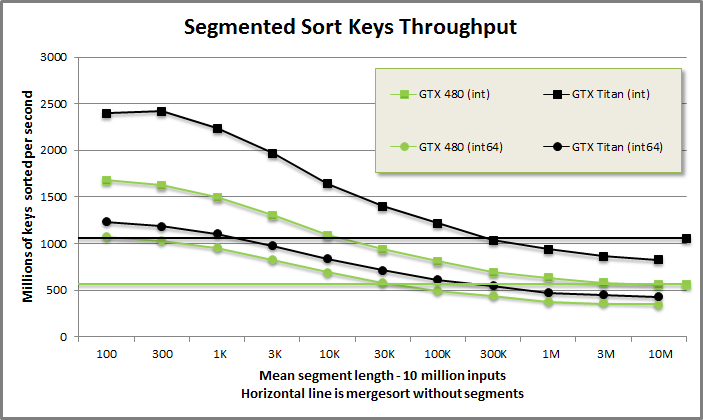
Segmented sort keys benchmark from benchmarksegsort/benchmarksegsort.cu
Segmented sort keys demonstration from tests/demo.cu
void DemoSegSortKeys(CudaContext& context) {
printf("\n\nSEG-SORT KEYS DEMONSTRATION:\n\n");
// Use CudaContext::GenRandom to generate 100 random integers between 0 and
// 9.
int N = 100;
MGPU_MEM(int) keys = context.GenRandom<int>(N, 0, 99);
// Define 10 segment heads (for 11 segments in all).
const int NumSegs = 10;
const int SegHeads[NumSegs] = { 4, 19, 22, 56, 61, 78, 81, 84, 94, 97 };
MGPU_MEM(int) segments = context.Malloc(SegHeads, 10);
printf("Input keys:\n");
PrintArray(*keys, "%4d", 10);
printf("\nSegment heads:\n");
PrintArray(*segments, "%4d", 10);
// Sort within segments.
SegSortKeysFromIndices(keys->get(), N, segments->get(), NumSegs, context);
printf("\nSorted data (segment heads are marked by *):\n");
PrintArrayOp(*keys, FormatOpMarkArray(" %c%2d", SegHeads, NumSegs), 10);
}SEG-SORT KEYS DEMONSTRATION:
Input keys:
0: 42 39 9 77 59 97 47 74 69 63
10: 69 7 63 63 3 52 6 29 31 32
20: 53 63 65 99 40 51 81 72 71 24
30: 96 33 53 74 32 68 10 68 61 7
40: 77 45 42 69 9 6 26 6 15 52
50: 28 26 44 48 52 13 45 9 87 12
60: 51 96 94 75 63 26 95 72 24 41
70: 67 47 28 5 67 61 69 49 6 90
80: 25 93 22 91 66 30 84 79 34 22
90: 78 44 67 51 0 23 60 71 38 98
Segment heads:
0: 4 19 22 56 61 78 81 84 94 97
Sorted data (segment heads are marked by *):
0: 9 39 42 77 * 3 6 7 29 31 47
10: 52 59 63 63 63 69 69 74 97 *32
20: 53 63 * 6 6 7 9 10 13 15 24
30: 26 26 28 32 33 40 42 44 45 48
40: 51 52 52 53 61 65 68 68 69 71
50: 72 74 77 81 96 99 * 9 12 45 51
60: 87 * 5 24 26 28 41 47 49 61 63
70: 67 67 69 72 75 94 95 96 * 6 25
80: 90 *22 91 93 *22 30 34 44 51 66
90: 67 78 79 84 * 0 23 60 *38 71 98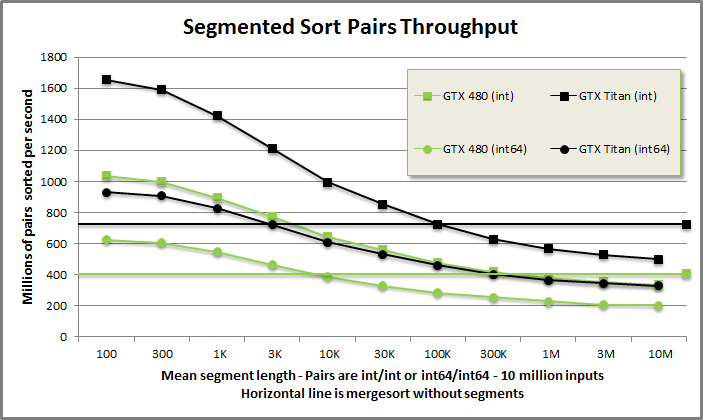
Segmented sort pairs benchmark from benchmarksegsort/benchmarksegsort.cu
Segmented sort pairs demonstration from tests/demo.cu
void DemoSegSortPairs(CudaContext& context) {
printf("\n\nSEG-SORT PAIRS DEMONSTRATION:\n\n");
// Use CudaContext::GenRandom to generate 100 random integers between 0 and
// 9.
int N = 100;
MGPU_MEM(int) keys = context.GenRandom<int>(N, 0, 99);
// Fill values with ascending integers.
MGPU_MEM(int) values = context.FillAscending<int>(N, 0, 1);
// Define 10 segment heads (for 11 segments in all).
const int NumSegs = 10;
const int SegHeads[NumSegs] = { 4, 19, 22, 56, 61, 78, 81, 84, 94, 97 };
MGPU_MEM(int) segments = context.Malloc(SegHeads, 10);
printf("Input keys:\n");
PrintArray(*keys, "%4d", 10);
printf("\nSegment heads:\n");
PrintArray(*segments, "%4d", 10);
// Sort within segments.
SegSortPairsFromIndices(keys->get(), values->get(), N, segments->get(),
NumSegs, context);
printf("\nSorted data (segment heads are marked by *):\n");
PrintArrayOp(*keys, FormatOpMarkArray(" %c%2d", SegHeads, NumSegs), 10);
printf("\nSorted indices (segment heads are marked by *):\n");
PrintArrayOp(*values, FormatOpMarkArray(" %c%2d", SegHeads, NumSegs), 10);
}SEG-SORT PAIRS DEMONSTRATION:
Input keys:
0: 91 65 0 27 46 46 42 0 46 44
10: 77 97 32 30 78 21 47 24 3 80
20: 17 48 72 40 47 21 15 54 34 72
30: 60 28 19 54 73 75 24 33 91 80
40: 26 85 76 1 18 88 28 59 9 8
50: 57 92 68 91 54 98 42 90 64 94
60: 64 93 67 0 63 77 94 2 20 58
70: 70 64 23 32 11 11 60 12 45 97
80: 45 53 66 66 77 70 35 6 66 20
90: 41 43 84 1 83 6 25 34 61 31
Segment heads:
0: 4 19 22 56 61 78 81 84 94 97
Sorted data (segment heads are marked by *):
0: 0 27 65 91 * 0 3 21 24 30 32
10: 42 44 46 46 46 47 77 78 97 *17
20: 48 80 * 1 8 9 15 18 19 21 24
30: 26 28 28 33 34 40 47 54 54 54
40: 57 59 60 68 72 72 73 75 76 80
50: 85 88 91 91 92 98 *42 64 64 90
60: 94 * 0 2 11 11 12 20 23 32 58
70: 60 63 64 67 70 77 93 94 *45 45
80: 97 *53 66 66 * 1 6 20 35 41 43
90: 66 70 77 84 * 6 25 83 *31 34 61
Sorted indices (segment heads are marked by *):
0: 2 3 1 0 * 7 18 15 17 13 12
10: 6 9 4 5 8 16 10 14 11 *20
20: 21 19 *43 49 48 26 44 32 25 36
30: 40 31 46 37 28 23 24 27 33 54
40: 50 47 30 52 22 29 34 35 42 39
50: 41 45 38 53 51 55 *56 58 60 57
60: 59 *63 67 74 75 77 68 72 73 69
70: 76 64 71 62 70 65 61 66 *78 80
80: 79 *81 82 83 *93 87 89 86 90 91
90: 88 85 84 92 *95 96 94 *99 97 98Locality sort keys benchmark from benchmarklocalitysort/benchmarklocalitysort.cu
Locality sort keys demonstration from tests/demo.cu
void DemoLocalitySortKeys(CudaContext& context) {
printf("\n\nLOCALITY SORT KEYS DEMONSTRATION:\n\n");
// Generate keys that are roughly sorted but with added noise.
int N = 100;
std::vector<int> keysHost(N);
for(int i = 0; i < N; ++i)
keysHost[i] = i + Rand(0, 25);
MGPU_MEM(int) keys = context.Malloc(keysHost);
printf("Input keys:\n");
PrintArray(*keys, "%4d", 10);
// Sort by exploiting locality.
LocalitySortKeys(keys->get(), N, context);
printf("\nSorted data:\n");
PrintArray(*keys, "%4d", 10);;
}LOCALITY SORT KEYS DEMONSTRATION:
Input keys:
0: 15 26 16 9 26 27 12 16 16 28
10: 13 32 36 18 30 40 28 35 34 44
20: 34 40 38 28 38 34 44 32 41 50
30: 55 55 37 52 36 57 38 48 39 47
40: 50 62 53 57 53 48 65 52 64 61
50: 70 61 76 72 79 64 60 77 61 84
60: 78 83 64 84 77 74 79 68 90 94
70: 82 92 82 95 91 76 95 77 91 94
80: 89 100 85 99 99 102 92 111 89 95
90: 109 114 98 96 105 103 113 119 107 105
Sorted data:
0: 9 12 13 15 16 16 16 18 26 26
10: 27 28 28 28 30 32 32 34 34 34
20: 35 36 36 37 38 38 38 39 40 40
30: 41 44 44 47 48 48 50 50 52 52
40: 53 53 55 55 57 57 60 61 61 61
50: 62 64 64 64 65 68 70 72 74 76
60: 76 77 77 77 78 79 79 82 82 83
70: 84 84 85 89 89 90 91 91 92 92
80: 94 94 95 95 95 96 98 99 99 100
90: 102 103 105 105 107 109 111 113 114 119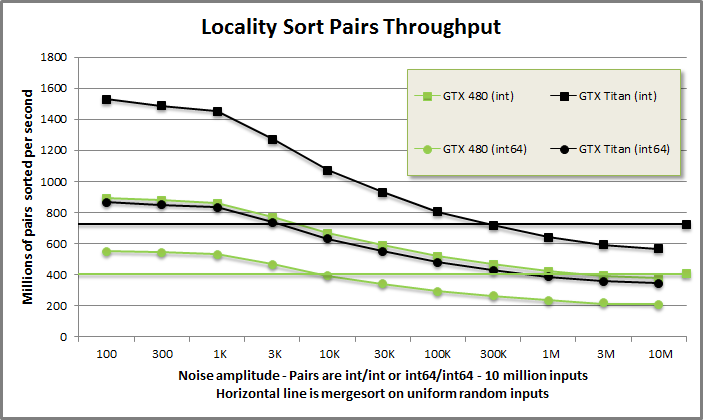
Locality sort pairs benchmark from benchmarklocalitysort/benchmarklocalitysort.cu
Locality sort pairs demonstration from tests/demo.cu
void DemoLocalitySortPairs(CudaContext& context) {
printf("\n\nLOCALITY SORT PAIRS DEMONSTRATION:\n\n");
// Generate keys that are roughly sorted but with added noise.
int N = 100;
std::vector<int> keysHost(N);
for(int i = 0; i < N; ++i)
keysHost[i] = i + Rand(0, 25);
MGPU_MEM(int) keys = context.Malloc(keysHost);
MGPU_MEM(int) values = context.FillAscending<int>(N, 0, 1);
printf("Input keys:\n");
PrintArray(*keys, "%4d", 10);
// Sort by exploiting locality.
LocalitySortPairs(keys->get(), values->get(), N, context);
printf("\nSorted data:\n");
PrintArray(*keys, "%4d", 10);
printf("\nSorted indices:\n");
PrintArray(*values, "%4d", 10);
}LOCALITY SORT PAIRS DEMONSTRATION:
Input keys:
0: 19 22 12 17 21 29 24 20 19 26
10: 10 14 20 38 25 31 23 21 23 20
20: 41 33 33 43 47 37 36 49 47 45
30: 40 54 53 33 53 53 45 52 43 41
40: 60 66 66 48 52 53 63 64 59 73
50: 71 56 71 77 58 77 78 68 83 71
60: 73 75 84 84 79 68 70 83 73 94
70: 80 87 91 84 95 75 96 79 86 92
80: 93 101 84 102 86 89 89 93 105 100
90: 102 102 96 110 106 99 99 101 99 101
Sorted data:
0: 10 12 14 17 19 19 20 20 20 21
10: 21 22 23 23 24 25 26 29 31 33
20: 33 33 36 37 38 40 41 41 43 43
30: 45 45 47 47 48 49 52 52 53 53
40: 53 53 54 56 58 59 60 63 64 66
50: 66 68 68 70 71 71 71 73 73 73
60: 75 75 77 77 78 79 79 80 83 83
70: 84 84 84 84 86 86 87 89 89 91
80: 92 93 93 94 95 96 96 99 99 99
90: 100 101 101 101 102 102 102 105 106 110
Sorted indices:
0: 10 2 11 3 0 8 7 12 19 4
10: 17 1 16 18 6 14 9 5 15 21
20: 22 33 26 25 13 30 20 39 23 38
30: 29 36 24 28 43 27 37 44 32 34
40: 35 45 31 51 54 48 40 46 47 41
50: 42 57 65 66 50 52 59 49 60 68
60: 61 75 53 55 56 64 77 70 58 67
70: 62 63 73 82 78 84 71 85 86 72
80: 79 80 87 69 74 76 92 95 96 98
90: 89 81 97 99 83 90 91 88 94 93//////////////////////////////////////////////////////////////////////////////// // kernels/segmentedsort.cuh // Mergesort count items in-place in data_global. Keys are compared with Comp // (as they are in MergesortKeys), however keys remain inside the segments // defined by flags_global. // flags_global is a bitfield cast to uint*. Each bit in flags_global is a // segment head flag. Only keys between segment head flags (inclusive on the // left and exclusive on the right) may be exchanged. The first element is // assumed to start a segment, regardless of the value of bit 0. // Passing verbose=true causes the function to print mergepass statistics to the // console. This may be helpful for developers to understand the performance // characteristics of the function and how effectively it early-exits merge // operations. template<typename T, typename Comp> MGPU_HOST void SegSortKeysFromFlags(T* data_global, int count, const uint* flags_global, CudaContext& context, Comp comp, bool verbose = false); // SegSortKeysFromFlags specialized with Comp = mgpu::less<T>. template<typename T> MGPU_HOST void SegSortKeysFromFlags(T* data_global, int count, const uint* flags_global, CudaContext& context, bool verbose = false); // Segmented sort using head flags and supporting value exchange. template<bool Stable, typename KeyType, typename ValType, typename Comp> MGPU_HOST void SegSortPairsFromFlags(KeyType* keys_global, ValType* values_global, const uint* flags_global, int count, CudaContext& context, Comp comp, bool verbose = false); // SegSortPairsFromFlags specialized with Comp = mgpu::less<T>. template<bool Stable, typename KeyType, typename ValType> MGPU_HOST void SegSortPairsFromFlags(KeyType* keys_global, ValType* values_global, const uint* flags_global, int count, CudaContext& context, bool verbose = false) // Segmented sort using segment indices rather than head flags. indices_global // is a sorted and unique list of indicesCount segment start locations. These // indices correspond to the set bits in the flags_global field. A segment // head index for position 0 may be omitted. template<typename T, typename Comp> MGPU_HOST void SegSortKeysFromIndices(T* data_global, int count, const int* indices_global, int indicesCount, CudaContext& context, Comp comp, bool verbose = false); // SegSortKeysFromIndices specialized with Comp = mgpu::less<T>. template<typename T> MGPU_HOST void SegSortKeysFromIndices(T* data_global, int count, const int* indices_global, int indicesCount, CudaContext& context, bool verbose = false); // Segmented sort using segment indices and supporting value exchange. template<typename KeyType, typename ValType, typename Comp> MGPU_HOST void SegSortPairsFromIndices(KeyType* keys_global, ValType* values_global, int count, const int* indices_global, int indicesCount, CudaContext& context, Comp comp, bool verbose = false); // SegSortPairsFromIndices specialized with Comp = mgpu::less<KeyType>. template<typename KeyType, typename ValType> MGPU_HOST void SegSortPairsFromIndices(KeyType* keys_global, ValType* values_global, int count, const int* indices_global, int indicesCount, CudaContext& context, bool verbose = false); //////////////////////////////////////////////////////////////////////////////// // kernels/localitysort.cuh // LocalitySortKeys is a version of MergesortKeys optimized for non-uniformly // random input arrays. If the keys begin close to their sorted destinations, // this function may exploit the structure to early-exit merge passes. // Passing verbose=true causes the function to print mergepass statistics to the // console. This may be helpful for developers to understand the performance // characteristics of the function and how effectively it early-exits merge // operations. template<typename T, typename Comp> MGPU_HOST void LocalitySortKeys(T* data_global, int count, CudaContext& context, Comp comp, bool verbose = false); // LocalitySortKeys specialized with Comp = mgpu::less<T>. template<typename T> MGPU_HOST void LocalitySortKeys(T* data_global, int count, CudaContext& context, bool verbose = false); // Locality sort supporting value exchange. template<typename KeyType, typename ValType, typename Comp> MGPU_HOST void LocalitySortPairs(KeyType* keys_global, ValType* values_global, int count, CudaContext& context, Comp comp, bool verbose = false); // LocalitySortPairs specialized with Comp = mpgu::less<T>. template<typename KeyType, typename ValType> MGPU_HOST void LocalitySortPairs(KeyType* keys_global, ValType* values_global, int count, CudaContext& context, bool verbose = false);
Segmented sort is the function that I expect to have the most immediate impact on people's applications. It addresses one facet of a serious problem facing GPU computing: we can often solve a single big problem but find it difficult to process many smaller problems in parallel.
What does the ad-hoc approach for sorting multiple variable-length arrays in parallel look like? We know how to sort keys in a thread using sorting networks. We know how to mergesort within a warp or block. MGPU Merge can take a coop parameter to merge small lists in parallel, as long as those lists are power-of-two multiples of the block size.
As a hypothetical, perhaps we could just sort within the segment intervals. Intervals shorter than VT would be processed by an intra-thread sorting network kernel. Intervals shorter than 32 * VT would be sorted by a warp-sorting kernel. Intervals shorter than NV would be sorted by our blocksort. We could use mergesort or radix sort on longer intervals, shifting segment IDs into the most-significant bits of the key, to maintain segment stability. After all these launches we'd re-order the data back into their original segment order.
But this would be a nightmare to write and maintain.
If all we want is simplicity, we could call mergesort on individual segments using CUDA Dynamic Parallelism on sm_35 devices. However this would cause severe load-balance issues. It would perform worse than a brute-force radix sort with segment identifiers fused to the keys. Performance would degrade with the segment size—small segments would be provisioned entire CTAs, wasting huge amounts of compute.
Not knowing how to finesse problems like this is why CUDA has a reputation of being hard to program. It is infuriating that the smaller a problem gets, the more desperate the solution becomes.
MGPU Segmented Sort makes a single observation, modifies our mergesort, and delivers an implementation that is elegant and fast.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 41 67 34 0 39 24 78 58 62 64 5 81 45 27 61 91 ^ ^ ^ ^
Consider these 16 random numbers grouped into four irregular segments. Segment heads are marked with carets. We're going to launch four tiny 'blocksorts' that sort four inputs each, maintaining segment order:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 41 67 34 0 39 24 78 58 62 64 5 81 45 27 61 91 ^ ^ ^ ^ Sort into blocks of length 4: 0 1 2 3 | 4 5 6 7 | 8 9 10 11 | 12 13 14 15 0 34 41 67 | 39 24 58 78 | 62 64 5 81 | 45 27 61 91 ^ ^ ^ ^
We use induction to explain the segmented blocksort above in terms of the merge operation illustrated below. Imagine a blocksort of segmented random data as a sequence of iterative merge operations, beginning with lists of length 4.
0 1 2 3 | 4 5 6 7 | 8 9 10 11 | 12 13 14 15 0 34 41 67 | 39 24 58 78 | 62 64 5 81 | 45 27 61 91 ^ ^ ^ ^ Merge list 0 (block 0) with list 1 (block 1) Merge list 2 (block 2) with list 3 (block 3): ( 0 1 2 3 | 4 5 6 7)|( 8 9 10 11 | 12 13 14 15) ( 0 34 39 41 | 67 24 58 78)|(62 64 5 45 | 81 27 61 91) ^ ^ ^ ^ Merge list 0 (blocks 0 and 1) with list 1 (blocks 2 and 3): ( 0 1 2 3 | 4 5 6 7 | 8 9 10 11 | 12 13 14 15) ( 0 34 39 41 | 67 24 58 62 | 64 78 5 45 | 81 27 61 91) ^ ^ ^ ^
In the coop = 2 stage, where two blocks cooperatively merge pairs of lists, the green segment that spans the block 0/block 1 boundary and the green segment that spans the block 2/block 3 boundary is modified. In the coop = 4 stage, where four blocks cooperatively merge pairs of lists, the black segment that spans the block 1/block 2 boundary is modified. This fully sorts the inputs.
The observation that enables efficient segmented sorting is that only segments that span the active interface between the two input lists are modified. The active interface is where the list on the left ends and the list on the right begins. During the coop = 2 stage, the portion of the first black segment being merged into list 0 cannot be mixed with data to its left because those terms belong to the green segment; it cannot be mixed with the portion of the same segment to the right, because that data is belongs to a different output list (the boundary between block 1 and block 2 isn't an active interface until the next merge stage).
During the coop = 2 stage, only the black segment in the middle - the one that spans the interface - is modified. The other three segments are simply copied directly from source to destination.
Important: When merging lists of segmented data, only elements in the segments that span the active interface between inputs lists is modified. All other segments are locked in place and their terms are copied directly from input to output.
template<int NT, int VT, bool Stable, bool HasValues, typename KeyType,
typename ValType, typename Comp>
MGPU_DEVICE int2 CTASegsort(KeyType threadKeys[VT], ValType threadValues[VT],
int tid, int headFlags, KeyType* keys_shared, ValType* values_shared,
int* ranges_shared, Comp comp) {
if(Stable)
// Odd-even transpose sort.
OddEvenTransposeSortFlags<VT>(threadKeys, threadValues, headFlags,
comp);
else
// Batcher's odd-even mergesort.
OddEvenMergesortFlags<VT>(threadKeys, threadValues, headFlags, comp);
// Record the first and last occurrence of head flags in this segment.
int blockEnd = 31 - clz(headFlags);
if(-1 != blockEnd) blockEnd += VT * tid;
int blockStart = ffs(headFlags);
blockStart = blockStart ? (VT * tid - 1 + blockStart) : (NT * VT);
ranges_shared[tid] = (int)bfi(blockEnd, blockStart, 16, 16);
// Store back to shared mem. The values are in VT-length sorted lists.
// These are merged recursively.
DeviceThreadToShared<VT>(threadKeys, tid, keys_shared);
int2 activeRange = CTASegsortLoop<NT, VT, HasValues>(threadKeys,
threadValues, keys_shared, values_shared, ranges_shared, tid,
make_int2(blockStart, blockEnd), comp);
return activeRange;
}CTASegsort is a reusable segmented blocksort and a generalization of CTAMergesort. The caller provides segment head flags packed into the bitfield headFlags. As shown in the section on sorting networks, the odd-even transposition network includes logic to support segmentation. It only swaps elements i and i+1 if the i+1 flag in the bitfield is cleared, meaning both elements are in the same segment. After the sorting network, the keys are in sorted lists with length VT.
For both segmented blocksort and the global merge passes, we build a binary tree of segment active ranges (the left- and right-most segment heads in a list). Only elements falling outside the active range can ever be modified by the sort. After the sorting network is run we calculate the active ranges (blockStart and blockEnd). We can now discard the head flags: the only necessary segment information for this sort is in the binary tree of ranges.
Threads use the CUDA instructions ffs (find first set) and clz (count leading zeros) to find the left-most and right-most segment heads in the list. These are referenced in the coordinate system of the CTA: if thread tid has a left-most segment head at 3, blockStart is assigned VT * tid + 3. If the thread doesn't contain a segment head, the interval (NV, -1) is used. The ranges are packed into a 32-bit integer with bfi (bitfield insert) and stored in the auxiliary array ranges_shared.
template<int NT, int VT, bool HasValues, typename KeyType, typename ValType,
typename Comp>
MGPU_DEVICE int2 CTASegsortLoop(KeyType threadKeys[VT],
ValType threadValues[VT], KeyType* keys_shared, ValType* values_shared,
int* ranges_shared, int tid, int2 activeRange, Comp comp) {
const int NumPasses = sLogPow2<NT>::value;
#pragma unroll
for(int pass = 0; pass < NumPasses; ++pass) {
int indices[VT];
CTASegsortPass<NT, VT>(keys_shared, ranges_shared, tid, pass,
threadKeys, indices, activeRange, comp);
if(HasValues) {
// Exchange values through shared memory.
DeviceThreadToShared<VT>(threadValues, tid, values_shared);
DeviceGather<NT, VT>(NT * VT, values_shared, indices, tid,
threadValues);
}
// Store results in shared memory in sorted order.
DeviceThreadToShared<VT>(threadKeys, tid, keys_shared);
}
return activeRange;
}CTASegsortLoop is a copy of CTABlocksortLoop which forwards to CTASegsortPass instead of CTABlocksortPass. The segmented sort very closely follows the vanilla mergesort, both for ease-of-maintenance reasons and to help illustrate how enacting one small improvement can bring huge functionality and performance benefits to an old and simple algorithm.
template<int NT, int VT, typename T, typename Comp>
MGPU_DEVICE void CTASegsortPass(T* keys_shared, int* ranges_shared, int tid,
int pass, T results[VT], int indices[VT], int2& activeRange, Comp comp) {
// Locate the intervals of the input lists.
int3 frame = FindMergesortFrame(2<< pass, tid, VT);
int a0 = frame.x;
int b0 = frame.y;
int listLen = frame.z;
int list = tid>> pass;
int listParity = 1 & list;
int diag = VT * tid - frame.x;
// Fetch the active range for the list this thread's list is merging with.
int siblingRange = ranges_shared[1 ^ list];
int siblingStart = 0x0000ffff & siblingRange;
int siblingEnd = siblingRange>> 16;
// Create a new active range for the merge.
int leftEnd = listParity ? siblingEnd : activeRange.y;
int rightStart = listParity ? activeRange.x : siblingStart;
activeRange.x = min(activeRange.x, siblingStart);
activeRange.y = max(activeRange.y, siblingEnd);
int p = SegmentedMergePath(keys_shared, a0, listLen, b0, listLen, leftEnd,
rightStart, diag, comp);
int a0tid = a0 + p;
int b0tid = b0 + diag - p;
SegmentedSerialMerge<VT>(keys_shared, a0tid, b0, b0tid, b0 + listLen,
results, indices, leftEnd, rightStart, comp);
// Store the ranges to shared memory.
if(0 == diag)
ranges_shared[list>> 1] =
(int)bfi(activeRange.y, activeRange.x, 16, 16);
}As in CTABlocksortPass, each thread in CTASegsortPass calculates the range of source values (the input lists) and its cross-diagonal within that list. As in the vanilla mergesort, the input list has coordinates (a0, a1), (b0, b1), and the output list has coordinates (a0, b1).
In addition, the segmented sort computes its list index, parity, and sibling. The index is the list that the thread is mapped into for that particular pass. For pass 0 (coop = 2), the index of thread tid is simply tid. The left- and right-most segment head positions are passed into activeRange.
tid (a0, a1) (b0, b1): diag list parity sibling
pass 0 (coop = 2):
0: ( 0, 7) ( 7, 14): 0 0 (0) 1
1: ( 0, 7) ( 7, 14): 7 1 (1) 0
2: (14, 21) (21, 28): 0 2 (0) 3
3: (14, 21) (21, 28): 7 3 (1) 2
4: (28, 35) (35, 42): 0 4 (0) 5
5: (28, 35) (35, 42): 7 5 (1) 4
6: (42, 49) (49, 56): 0 6 (0) 7
7: (42, 49) (49, 56): 7 7 (1) 6
pass 1 (coop = 4):
0: ( 0, 14) (14, 28): 0 0 (0) 1
1: ( 0, 14) (14, 28): 7 0 (0) 1
2: ( 0, 14) (14, 28): 14 1 (1) 0
3: ( 0, 14) (14, 28): 21 1 (1) 0
4: (28, 42) (42, 56): 0 2 (0) 3
5: (28, 42) (42, 56): 7 2 (0) 3
6: (28, 42) (42, 56): 14 3 (1) 2
7: (28, 42) (42, 56): 21 3 (1) 2
pass 2 (coop = 8):
0: ( 0, 28) (28, 56): 0 0 (0) 1
1: ( 0, 28) (28, 56): 7 0 (0) 1
2: ( 0, 28) (28, 56): 14 0 (0) 1
3: ( 0, 28) (28, 56): 21 0 (0) 1
4: ( 0, 28) (28, 56): 28 1 (1) 0
5: ( 0, 28) (28, 56): 35 1 (1) 0
6: ( 0, 28) (28, 56): 42 1 (1) 0
7: ( 0, 28) (28, 56): 49 1 (1) 0The list parity indicates what side of the merge a thread maps to: 0 for left and 1 for right. The other list in the merge is called sibling, and it has the opposite parity. Each thread loads the packed range of its sibling list from shared memory: this is the list it is merging with. The left and right ranges are merged together to find the left- and right-most segment heads of the resulting merged list. After the segmented merge, this is stored in shared memory and recursively percolated up, building the binary tree of active ranges.
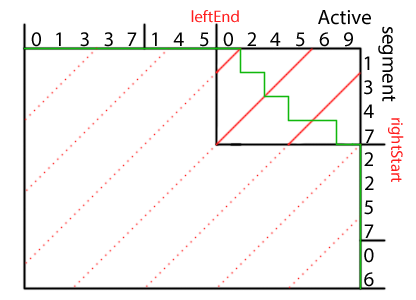
In CTASegsortPass, leftEnd is the location of the right-most segment in the left input list (drawn across the top of the diagram) and rightStart the location of the left-most segment in the right list (drawn along the right side). These define the ends of the active segment. For the area outside of (leftEnd, rightStart), the Merge Path follows the x- or y-axis, as it simply copies elements from one of the inputs. The cross-diagonals are constrained to the active segment region—queries outside this region return immediately.
template<typename InputIt, typename Comp>
MGPU_HOST_DEVICE int SegmentedMergePath(InputIt keys, int aOffset, int aCount,
int bOffset, int bCount, int leftEnd, int rightStart, int diag, Comp comp) {
// leftEnd and rightStart are defined from the origin, and diag is defined
// from aOffset.
// We only need to run a Merge Path search if the diagonal intersects the
// segment that strides the left and right halves (i.e. is between leftEnd
// and rightStart).
if(aOffset + diag <= leftEnd) return diag;
if(aOffset + diag >= rightStart) return aCount;
bCount = min(bCount, rightStart - bOffset);
int begin = max(max(leftEnd - aOffset, 0), diag - bCount);
int end = min(diag, aCount);
while(begin < end) {
int mid = (begin + end)>> 1;
int ai = aOffset + mid;
int bi = bOffset + diag - 1 - mid;
bool pred = !comp(keys[bi], keys[ai]);
if(pred) begin = mid + 1;
else end = mid;
}
return begin;
}SegmentedMergePath is a straight-forward modification of the MergePath binary search that clamps the cross-diagonals to the area defined by the active range.
template<int VT, typename T, typename Comp>
MGPU_DEVICE void SegmentedSerialMerge(const T* keys_shared, int aBegin,
int aEnd, int bBegin, int bEnd, T results[VT], int indices[VT],
int leftEnd, int rightStart, Comp comp, bool sync = true) {
bEnd = min(rightStart, bEnd);
T aKey = keys_shared[aBegin];
T bKey = keys_shared[bBegin];
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool p;
// If A has run out of inputs, emit B.
if(aBegin >= aEnd)
p = false;
else if(bBegin >= bEnd || aBegin < leftEnd)
// B has hit the end of the middle segment.
// Emit A if A has inputs remaining in the middle segment.
p = true;
else
// Emit the smaller element in the middle segment.
p = !comp(bKey, aKey);
results[i] = p ? aKey : bKey;
indices[i] = p ? aBegin : bBegin;
if(p) aKey = keys_shared[++aBegin];
else bKey = keys_shared[++bBegin];
}
if(sync) { __syncthreads(); }
}Four conditionals are evaluated when computing the merge predicate:
If aBegin >= aEnd the A pointer is out-of-range so we emit the next element in B.
If bBegin >= bEnd the B pointer is out-of-range or has hit the end of the active segment in the B list, if one exists. If the former is true, we simply emit A. If the latter is true, A must have at least entered the active segment (since A and B enter the active segment together), and A needs to complete emitting elements of the active segment before B can proceed to copy members of its inactive segments. Because the end of A's part of the active segment is also the end of A's input (see the illustration), once A finishes emitting its portion of the active segment, the first predicate, aBegin >= aEnd, succeeds, so all remaining trips through the loop evaluate p to false, so B's inactive segments are streamed out.
If aBegin < leftEnd the A pointer hasn't hit the start of its active segment. To preserve segment stability, all of A's segments are emitted before merging elements of B.
Otherwise, both pointers are inside the active segment. The keys are compared and the appropriate pointer is advanced, as in an ordinary merge.
We recursively merge lists, doubling their size and halving their number with each iteration. Since the number of active segments per merge remains fixed at one (that is, the segment on the active interface), the proportion of segments that are active vanishes as the sort progresses.
Tiles that map over only non-active segments (that is, segments to the left of the right-most segment head for tiles in the left half of the merge; and segments to right of the left-most segment head for tiles in the right half of the merge) do not require any merging. These stationary tiles check a copy flag: if the flag is set, the destination is up-to-date, and there is a no-op; if the flag is not set, the kernel copies from the source to the destination and sets the up-to-date flag. Tiles that map over an active segment clear the up-to-date flag and enqueue a merge operation.
Mean segment length = 300
Merge tiles Copy tiles
pass 0: 7098 ( 99.93%) 5 ( 0.07%)
pass 1: 4443 ( 62.55%) 2658 ( 37.42%)
pass 2: 2347 ( 33.04%) 3409 ( 47.99%)
pass 3: 1168 ( 16.44%) 2275 ( 32.03%)
pass 4: 572 ( 8.05%) 1168 ( 16.44%)
pass 5: 302 ( 4.25%) 572 ( 8.05%)
pass 6: 163 ( 2.29%) 302 ( 4.25%)
pass 7: 78 ( 1.10%) 163 ( 2.29%)
pass 8: 37 ( 0.52%) 78 ( 1.10%)
pass 9: 18 ( 0.25%) 37 ( 0.52%)
pass 10: 7 ( 0.10%) 18 ( 0.25%)
pass 11: 6 ( 0.08%) 7 ( 0.10%)
pass 12: 2 ( 0.03%) 6 ( 0.08%)
average: 1249 ( 17.59%) 822 ( 11.59%)
total : 16241 (228.65%) 10698 (150.61%)
Mean segment length = 10000
Merge tiles Copy tiles
pass 0: 7102 ( 99.99%) 1 ( 0.01%)
pass 1: 6927 ( 97.52%) 176 ( 2.48%)
pass 2: 6639 ( 93.47%) 372 ( 5.24%)
pass 3: 6022 ( 84.78%) 831 ( 11.70%)
pass 4: 5019 ( 70.66%) 1508 ( 21.23%)
pass 5: 3758 ( 52.91%) 2084 ( 29.34%)
pass 6: 2217 ( 31.21%) 2625 ( 36.96%)
pass 7: 1329 ( 18.71%) 1892 ( 26.64%)
pass 8: 619 ( 8.71%) 1329 ( 18.71%)
pass 9: 232 ( 3.27%) 619 ( 8.71%)
pass 10: 110 ( 1.55%) 232 ( 3.27%)
pass 11: 148 ( 2.08%) 110 ( 1.55%)
pass 12: 88 ( 1.24%) 148 ( 2.08%)
average: 3093 ( 43.55%) 917 ( 12.92%)
total : 40210 (566.10%) 11927 (167.91%)SegmentedSort launch with verbose = true work reporting
The coarse-grained partitioning kernel used by MGPU Merge and Mergesort is augmented to also enqueue merge and copy work-items. The number of merge and copy tasks for a segmented sort grows with the mean segment length. In the above figure, the number of enqueued merge and copy operations is printed for each pass, for 10,000,000 inputs with average segment lengths of 300 and 10000 elements.
Once the merged list length exceeds the mean segment length, the number of merge operations required each pass begins to decrease by powers of two. The case with segment length of 300 exhibits this geometric decrease after the first global merge pass; the entire sort only requires the equivalent of only 2.28 global passes over the data. For the case with segment length of 10,000, this geometric decrease in workload takes longer to manifest, and 5.66 passes are required to sort the data.
Although this same early-exit tactic could be used within the segmented blocksort, we wouldn't expect an equivalent increase in performance there. Threads that discover that they're mapped over only non-active segments could choose to no-op, but due to SIMD execution rules, a diverged warp runs only as fast as its slowest lane. It may be feasible to dynamically reconfigure the segmented blocksort to benefit from early-exit, but that is beyond the scope of this effort.
During the global merge passes, tiles that map over fully-sorted segments (or any other 'stable' data) can early-exit rather than merging. Only CTAs that map over "active segments" (segments straddling the merge interface of two sorted input lists) need to be merged. Since the number of active segments decrees geometrically (the number of lists is cut in half each iteration as the length of the lists double), a geometrically increasing percentage of CTAs may early-exit. We implement a special work-queueing system to process active tiles on a fixed-size launch of persistent CTAs—this eliminates the start-up cost for CTAs that simply exit out.
Mergesort is an out-of-place operation. After blocksorting we load from one buffer and store to another, swap, and repeat until the data is fully sorted. A temporary buffer is allocated with enough capacity to hold a flag per tile. If the domain of the tile has the same elements in both of the double buffers, the flag is set. Early-exit with tile granularity is enabled by this status flag: if the flag is set and the tile source interval maps to the destination interval, the tile operation can be elided.
The work-queueing system supports two different operations on tiles:
Merge - If the tile's source interval (as returned by ComputeMergeRange) does not map directly into the destination interval, we merge the two source lists and clear the tile's status flag.
Copy - If the tile's source interval maps directly into the destination interval and the status flag is cleared (indicating the source and destination tile ranges do not contain the same elements), the source interval is copied to the destination and the status flag is set.
Each global merge pass launches two kernels: the first performs global partitioning and schedules merge and copy tasks by pushing to two work queues; the second cooperatively executes all queued merge and copy tasks.
include/kernels/segmentedsort.cuh
template<int NT, bool Segments, typename KeyType, typename Comp>
__global__ void KernelSegSortPartitionBase(const KeyType* keys_global,
SegSortSupport support, int count, int nv, int numPartitions, Comp comp) {
union Shared {
int partitions[NT];
typename CTAScan<NT, ScanOpAdd>::Storage scan;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int partition = tid + (NT - 1) * blockIdx.x;
// Compute one extra partition per CTA. If the CTA size is 128 threads, we
// compute 128 partitions and 127 blocks. The next CTA then starts at
// partition 127 rather than 128. This relieves us from having to launch
// a second kernel to build the work queues.
int p0;
int3 frame;
if(partition < numPartitions) {
frame = FindMergesortFrame(2, partition, nv);
int listLen = frame.z;
int a0 = frame.x;
int b0 = min(frame.y, count);
int diag = nv * partition - a0;
int aCount = min(listLen, count - a0);
int bCount = min(listLen, count - b0);
if(Segments) {
// Segmented merge path calculation. Use the ranges as constraints.
int leftRange = support.ranges_global[~1 & partition];
int rightRange = support.ranges_global[
min(numPartitions - 2, 1 | partition)];
// Unpack the left and right ranges. Transform them into the global
// coordinate system by adding a0 or b0.
int leftStart = 0x0000ffff & leftRange;
int leftEnd = leftRange>> 16;
if(nv == leftStart) leftStart = count;
else leftStart += a0;
if(-1 != leftEnd) leftEnd += a0;
int rightStart = 0x0000ffff & rightRange;
int rightEnd = rightRange>> 16;
if(nv == rightStart) rightStart = count;
else rightStart += b0;
if(-1 != rightEnd) rightEnd += b0;
if(0 == diag)
support.ranges2_global[partition>> 1] = make_int2(
min(leftStart, rightStart),
max(leftEnd, rightEnd));
p0 = SegmentedMergePath(keys_global, a0, aCount, b0, bCount,
leftEnd, rightStart, diag, comp);
} else
// Unsegmented merge path search.
p0 = MergePath<MgpuBoundsLower>(keys_global + a0, aCount,
keys_global + b0, bCount, diag, comp);
shared.partitions[tid] = p0;
}
__syncthreads();
bool active = (tid < NT - 1) && (partition < numPartitions - 1);
int p1 = active ? shared.partitions[tid + 1] : 0;
__syncthreads();
DeviceSegSortCreateJob<NT>(support, count, active, frame, tid, 0, nv,
partition, p0, p1, shared.partitions);
}After launching the segmented blocksort, the host launches KernelSegSortPartitionBase for the first global merge pass or KernelSegSortPartitionDerived for all subsequent passes. Each thread computes one partition, but since a tile needs both a starting and ending partition, a CTA of NT threads can enqueue only NT - 1 tiles.
For the base-pass kernel above, the 16-bit active ranges for each blocksort tile are unpacked and transformed by addition from tile-local coordinates to global coordinates. Neighboring active ranges (covering the two sorted lists that serve as sources for the sort's first merge pass) are then stored as int2 types in support.ranges2_global, into which a binary tree of active ranges is constructed; this corresponds exactly to the active-range tree constructed by CTASegsortPass in the segmented blocksort.
SegmentedMergePath searches global data for the intersection of the Merge Path and the thread's cross-diagonal. If the cross-diagonal does not pass through the active segment (like any of the cross-diagonals that intersect the A- and B-axes as dotted lines in the segmented Merge Path figure above), the search returns immediately. As we progress in the mergesort, the percentage of cross-diagonals intersecting the active list vanishes, and we effectively benefit from early-exit of partitioning in addition to merging.
include/kernels/segmentedsort.cuh
template<int NT>
MGPU_DEVICE void DeviceSegSortCreateJob(SegSortSupport support,
int count, bool active, int3 frame, int tid, int pass, int nv, int block,
int p0, int p1, int* shared) {
typedef CTAScan<NT, ScanOpAdd> S;
typename S::Storage* scan = (typename S::Storage*)shared;
// Compute the gid'th work time.
bool mergeOp = false;
bool copyOp = false;
int gid = nv * block;
int4 mergeRange;
if(active) {
int4 range = FindMergesortInterval(frame, 2<< pass, block, nv, count,
p0, p1);
int a0 = range.x;
int a1 = range.y;
int b0 = range.z;
int b1 = range.w;
if(a0 == a1) {
a0 = b0;
a1 = b1;
b0 = b1;
}
mergeRange = make_int4(a0, a1, b0, block);
mergeOp = (b1 != b0) || (a0 != gid);
copyOp = !mergeOp && (!pass || !support.copyStatus_global[block]);
}
int mergeTotal, copyTotal;
int mergeScan = S::Scan(tid, mergeOp, *scan, &mergeTotal);
int copyScan = S::Scan(tid, copyOp, *scan, ©Total);
if(!tid) {
shared[0] = atomicAdd(&support.queueCounters_global->x, mergeTotal);
shared[1] = atomicAdd(&support.queueCounters_global->y, copyTotal);
}
__syncthreads();
if(mergeOp) {
support.copyStatus_global[block] = 0;
support.mergeList_global[shared[0] + mergeScan] = mergeRange;
}
if(copyOp) {
support.copyStatus_global[block] = 1;
support.copyList_global[shared[1] + copyScan] = block;
}
}DeviceSegSortCreateJob is called at the end of both partition kernels. This is where we put the early-exit logic. The function is passed the begin and end Merge Path indices. FindMergesortInterval takes the Merge Path indices and computes the intervals that serve as the A and B input lists. If either A or B interval is empty, then we're loading from just one input. Since both inputs are sorted (remember we are merging pairs of sorted lists), then the tile is already sorted. In this case we elide the merge operation.
If we're on the first pass or copyStatus_global[block] is false, then the destination buffer doesn't have the same data as the source buffer over the tile's output interval. We enqueue a copy operation by stepping on atomicAdd and storing the tile index to copy to copyList_global. If neither source interval is empty we must enqueue a merge by pushing the work interval to mergeList_global and clear the status bit.
Important: The early-exit heuristic examines only the mapping of the source lists into each tile. Early-exit does not require segmentation. Segmentation is a statement of sortedness in the input, but if keys were passed in the same relative order without providing segment indices, the early-exit behavior would be identical.
Locality sort is a specialization of segmented sort that does not support (or bear the costs of) segmentation. It uses the same partitioning and queueing kernels as segmented sort, but takes a branch that uses the standard Merge Path search. Locality sort also uses the standard mergesort blocksort. Use locality sort when inputs start near to their output locations. This is a qualititative characterization of a dataset. Programmers are encouraged to try both vanilla mergesort and locality sort and use the variant with the higher throughput.
include/kernels/segmentedsort.cuh
template<typename Tuning, bool Segments, bool HasValues, typename KeyType,
typename ValueType, typename Comp>
MGPU_LAUNCH_BOUNDS void KernelSegSortMerge(const KeyType* keys_global,
const ValueType* values_global, SegSortSupport support, int count,
int pass, KeyType* keysDest_global, ValueType* valsDest_global, Comp comp) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
union Shared {
KeyType keys[NT * (VT + 1)];
int indices[NV];
int4 range;
};
__shared__ Shared shared;
int tid = threadIdx.x;
// Check for merge work.
while(true) {
if(!tid) {
int4 range = make_int4(-1, 0, 0, 0);
int next = atomicAdd(&support.queueCounters_global->x, -1) - 1;
if(next >= 0) range = support.mergeList_global[next];
shared.range = range;
}
__syncthreads();
int4 range = shared.range;
__syncthreads();
if(range.x < 0) break;
int block = range.w;
int gid = NV * block;
int count2 = min(NV, count - gid);
range.w = count2 - (range.y - range.x) + range.z;
if(Segments)
// Segmented merge
DeviceSegSortMerge<NT, VT, HasValues>(keys_global, values_global,
support, tid, block, range, pass, shared.keys, shared.indices,
keysDest_global, valsDest_global, comp);
else
// Unsegmented merge (from device/ctamerge.cuh)
DeviceMerge<NT, VT, HasValues>(keys_global, values_global,
keys_global, values_global, tid, block, range, shared.keys,
shared.indices, keysDest_global, valsDest_global, comp);
}
// Check for copy work.
while(true) {
if(!tid) {
int list = -1;
int next = atomicAdd(&support.queueCounters_global->y, -1) - 1;
if(next >= 0) list = support.copyList_global[next];
shared.range.x = list;
}
__syncthreads();
int listBlock = shared.range.x;
__syncthreads();
if(listBlock < 0) break;
DeviceSegSortCopy<NT, VT, HasValues>(keys_global, values_global,
tid, listBlock, count, keysDest_global, valsDest_global);
}
}
Typically we size a grid launch to the data size. Because early-exit dynamically sizes the tasks, we'd have to copy task counts from device to host memory each iteration to change the launch size. This would synchronize the device and hurt performance. Instead we launch a fixed number of "persistent CTAs" (a small multiple of the number of SMs, queried with CudaContext::NumSMs()) and atomically peel tasks off the queues until both queues are empty.
All threads loop until the merge queue is empty, then loop until the copy queue is empty. Thread 0 decrements the queue counter and stores a code in shared memory. After synchronization, all threads read this code out and act accordingly.
Locality sort is supported by settings Segments = false: this directs the kernel to use DeviceMerge rather than DeviceSegSortMerge.