
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Run many concurrent searches where both the needles and haystack arrays are sorted. This input condition lets us recast the function as a sequential process resembling merge, rather than as a traditional binary search. Complexity improves from A log B to A + B, and because we touch every input, a search can retrieve not just the lower-bound of A into B but simultaneously the upper-bound of B into A, plus flags for all elements indicating if matches in the other array exist.

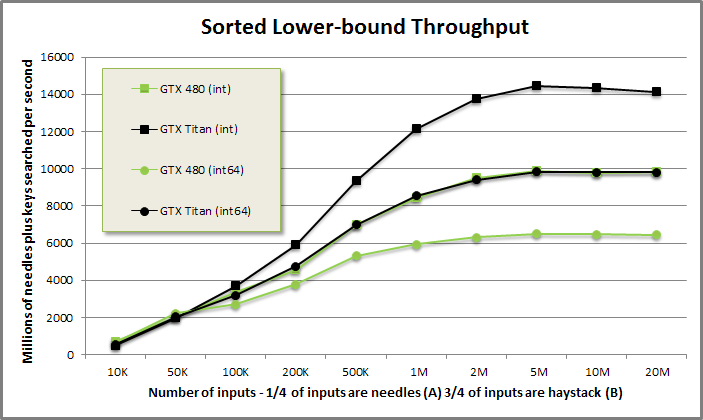
Vectorized sorted search (lower_bound A into B) benchmark from benchmarksortedsearch/benchmarksortedsearch.cu
Vectorized sorted search demostration from tests/demo.cu
void DemoSortedSearch(CudaContext& context) {
printf("\n\nSORTED SEARCH DEMONSTRATION:\n\n");
// Use CudaContext::SortRandom to generate a haystack of 200 random integers
// between 0 and 999 and an array of 100 needles in the same range.
int HaystackSize = 200;
int NeedlesSize = 100;
MGPU_MEM(int) haystack = context.SortRandom<int>(HaystackSize, 0, 299);
MGPU_MEM(int) needles = context.SortRandom<int>(NeedlesSize, 0, 299);
printf("Haystack array:\n");
PrintArray(*haystack, "%4d", 10);
printf("\nNeedles array:\n");
PrintArray(*needles, "%4d", 10);
// Run a vectorized sorted search to find lower bounds.
SortedSearch<MgpuBoundsLower>(needles->get(), NeedlesSize, haystack->get(),
HaystackSize, needles->get(), context);
printf("\nLower bound array:\n");
PrintArray(*needles, "%4d", 10);
}SORTED SEARCH DEMONSTRATION:
Haystack array:
0: 0 5 5 7 7 7 7 8 9 9
10: 10 11 12 14 15 15 16 17 19 19
20: 20 24 25 28 28 29 31 33 36 36
30: 37 38 40 42 42 43 45 46 49 50
40: 51 51 51 52 53 55 56 57 60 60
50: 61 61 62 62 64 66 68 69 73 74
60: 79 81 82 84 85 88 90 90 95 97
70: 99 101 105 108 108 111 115 118 118 119
80: 119 119 119 122 122 123 125 126 126 130
90: 133 133 135 135 139 140 143 145 145 146
100: 147 149 149 149 154 158 160 161 165 166
110: 168 169 170 172 172 174 174 174 175 175
120: 175 177 179 182 183 184 186 187 188 190
130: 192 193 194 196 198 199 199 205 205 208
140: 209 215 217 218 218 218 220 220 221 221
150: 223 224 225 230 234 234 235 240 240 243
160: 244 249 250 251 252 253 253 254 255 255
170: 255 257 258 258 259 262 263 265 267 270
180: 270 274 278 278 278 279 280 281 284 284
190: 284 285 285 292 294 295 296 296 296 298
Needles array:
0: 3 3 12 16 16 17 17 19 20 21
10: 24 27 27 28 30 31 35 39 40 42
20: 52 52 53 53 54 55 57 58 62 63
30: 72 75 83 86 86 89 92 95 98 98
40: 99 99 99 100 104 105 107 109 110 111
50: 112 117 118 121 124 126 129 132 133 139
60: 140 148 156 160 161 167 168 173 179 186
70: 191 198 202 202 212 212 214 220 223 229
80: 233 239 245 254 256 256 260 268 269 269
90: 271 271 272 273 277 285 296 296 299 299
Lower bound array:
0: 1 1 12 16 16 17 17 18 20 21
10: 21 23 23 23 26 26 28 32 32 33
20: 43 43 44 44 45 45 47 48 52 54
30: 58 60 63 65 65 66 68 68 70 70
40: 70 70 70 71 72 72 73 75 75 75
50: 76 77 77 83 86 87 89 90 90 94
60: 95 101 105 106 107 110 110 115 122 126
70: 130 134 137 137 141 141 141 146 150 153
80: 154 157 161 167 171 171 175 179 179 179
90: 181 181 181 181 182 191 196 196 200 200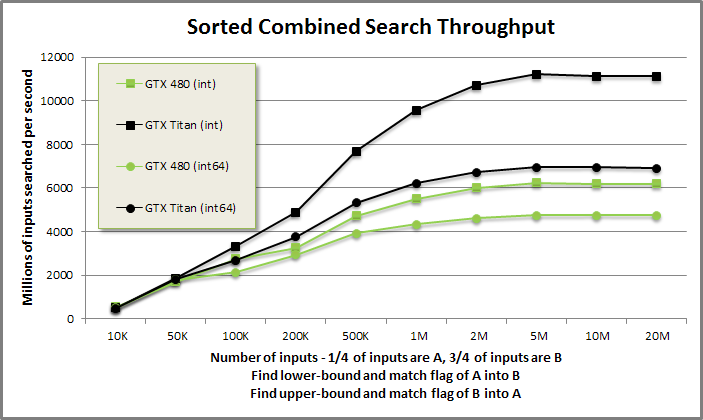
Vectorized sorted search (complete search) benchmark from benchmarksortedsearch/benchmarksortedsearch.cu
Vectorized sorted search demostration (2) from tests/demo.cu
void DemoSortedSearch2(CudaContext& context) {
printf("\n\nSORTED SEARCH DEMONSTRATION (2):\n\n");
int ACount = 100;
int BCount = 100;
MGPU_MEM(int) aData = context.SortRandom<int>(ACount, 0, 299);
MGPU_MEM(int) bData = context.SortRandom<int>(BCount, 0, 299);
MGPU_MEM(int) aIndices = context.Malloc<int>(ACount);
MGPU_MEM(int) bIndices = context.Malloc<int>(BCount);
printf("A array:\n");
PrintArray(*aData, "%4d", 10);
printf("\nB array:\n");
PrintArray(*bData, "%4d", 10);
// Run a vectorized sorted search to find lower bounds.
SortedSearch<MgpuBoundsLower, MgpuSearchTypeIndexMatch,
MgpuSearchTypeIndexMatch>(aData->get(), ACount, bData->get(), BCount,
aIndices->get(), bIndices->get(), context);
printf("\nLower bound of A into B (* for match):\n");
PrintArrayOp(*aIndices, FormatOpMaskBit("%c%3d"), 10);
printf("\nUpper bound of B into A (* for match):\n");
PrintArrayOp(*bIndices, FormatOpMaskBit("%c%3d"), 10);
}SORTED SEARCH DEMONSTRATION (2):
A array:
0: 0 3 5 13 14 15 16 18 18 21
10: 24 26 26 30 31 32 38 38 38 40
20: 60 72 72 74 81 83 86 88 88 89
30: 89 99 99 101 101 102 114 115 118 118
40: 119 128 136 139 145 148 149 150 151 151
50: 157 160 164 165 167 177 181 181 182 182
60: 189 190 191 192 196 197 199 200 207 212
70: 213 213 216 218 220 222 223 228 231 233
80: 233 234 234 234 239 239 240 247 249 264
90: 265 267 271 271 275 277 282 284 293 298
B array:
0: 1 2 15 23 24 25 25 25 25 27
10: 27 29 30 31 33 33 35 39 45 49
20: 58 59 61 61 62 63 64 67 67 68
30: 70 71 82 85 87 87 88 91 98 98
40: 109 110 110 116 116 118 121 121 126 129
50: 129 134 145 155 159 165 174 174 179 181
60: 183 186 192 192 196 196 201 202 204 205
70: 205 208 209 212 216 218 220 222 224 227
80: 231 233 233 234 235 236 250 251 251 253
90: 260 263 272 275 276 285 289 291 291 293
Lower bound of A into B (* for match):
0: 0 2 2 2 2 * 2 3 3 3 3
10: * 4 9 9 * 12 * 13 14 17 17 17 18
20: 22 32 32 32 32 33 34 * 36 * 36 37
30: 37 40 40 40 40 40 43 43 * 45 * 45
40: 46 49 52 52 * 52 53 53 53 53 53
50: 54 55 55 * 55 56 58 * 59 * 59 60 60
60: 62 62 62 * 62 * 64 66 66 66 71 * 73
70: 74 74 * 74 * 75 * 76 * 77 78 80 * 80 * 81
80: * 81 * 83 * 83 * 83 86 86 86 86 86 92
90: 92 92 92 92 * 93 95 95 95 * 99 100
Upper bound of B into A (* for match):
0: 1 1 * 6 10 * 11 11 11 11 11 13
10: 13 13 * 14 * 15 16 16 16 19 20 20
20: 20 20 21 21 21 21 21 21 21 21
30: 21 21 25 26 27 27 * 29 31 31 31
40: 36 36 36 38 38 * 40 41 41 41 42
50: 42 42 * 45 50 51 * 54 55 55 56 * 58
60: 60 60 * 64 * 64 * 65 * 65 68 68 68 68
70: 68 69 69 * 70 * 73 * 74 * 75 * 76 77 77
80: * 79 * 81 * 81 * 84 84 84 89 89 89 89
90: 89 89 94 * 95 95 98 98 98 98 * 99////////////////////////////////////////////////////////////////////////////////
// kernels/sortedsearch.cuh
// Vectorized sorted search. This is the most general form of the function.
// Executes two simultaneous linear searches on two sorted inputs.
// Bounds:
// MgpuBoundsLower -
// lower-bound search of A into B.
// upper-bound search of B into A.
// MgpuBoundsUpper -
// upper-bound search of A into B.
// lower-bound search of B into A.
// Type[A|B]:
// MgpuSearchTypeNone - no output for this input.
// MgpuSearchTypeIndex - return search indices as integers.
// MgpuSearchTypeMatch - return 0 (no match) or 1 (match).
// For TypeA, returns 1 if there is at least 1 matching element in B
// for element in A.
// For TypeB, returns 1 if there is at least 1 matching element in A
// for element in B.
// MgpuSearchTypeIndexMatch - return search indices as integers. Most
// significant bit is match bit.
// aMatchCount, bMatchCount - If Type is Match or IndexMatch, return the total
// number of elements in A or B with matches in B or A, if the pointer is
// not null. This generates a synchronous cudaMemcpyDeviceToHost call that
// callers using streams should be aware of.
template<MgpuBounds Bounds, MgpuSearchType TypeA, MgpuSearchType TypeB,
typename InputIt1, typename InputIt2, typename OutputIt1,
typename OutputIt2, typename Comp>
MGPU_HOST void SortedSearch(InputIt1 a_global, int aCount, InputIt2 b_global,
int bCount, OutputIt1 aIndices_global, OutputIt2 bIndices_global,
Comp comp, CudaContext& context, int* aMatchCount = 0,
int* bMatchCount = 0);
// SortedSearch specialized with Comp = mgpu::less<T>.
template<MgpuBounds Bounds, MgpuSearchType TypeA, MgpuSearchType TypeB,
typename InputIt1, typename InputIt2, typename OutputIt1,
typename OutputIt2>
MGPU_HOST void SortedSearch(InputIt1 a_global, int aCount, InputIt2 b_global,
int bCount, OutputIt1 aIndices_global, OutputIt2 bIndices_global,
CudaContext& context, int* aMatchCount = 0, int* bMatchCount = 0);
// SortedSearch specialized with
// TypeA = MgpuSearchTypeIndex
// TypeB = MgpuSearchTypeNone
// aMatchCount = bMatchCount = 0.
template<MgpuBounds Bounds, typename InputIt1, typename InputIt2,
typename OutputIt, typename Comp>
MGPU_HOST void SortedSearch(InputIt1 a_global, int aCount, InputIt2 b_global,
int bCount, OutputIt aIndices_global, Comp comp, CudaContext& context);
// SortedSearch specialized with Comp = mgpu::less<T>.
template<MgpuBounds Bounds, typename InputIt1, typename InputIt2,
typename OutputIt>
MGPU_HOST void SortedSearch(InputIt1 a_global, int aCount, InputIt2 b_global,
int bCount, OutputIt aIndices_global, CudaContext& context);
// SortedEqualityCount returns the difference between upper-bound (computed by
// this function) and lower-bound (passed as an argument). That is, it computes
// the number of occurences of a key in B that match each key in A.
// The provided operator must have a method:
// int operator()(int lb, int ub) const;
// It returns the count given the lower- and upper-bound indices.
//
// An object SortedEqualityOp is provided:
// struct SortedEqualityOp {
// MGPU_HOST_DEVICE int operator()(int lb, int ub) const {
// return ub - lb;
// }
// };
template<typename InputIt1, typename InputIt2, typename InputIt3,
typename OutputIt, typename Comp, typename Op>
MGPU_HOST void SortedEqualityCount(InputIt1 a_global, int aCount,
InputIt2 b_global, int bCount, InputIt3 lb_global, OutputIt counts_global,
Comp comp, Op op, CudaContext& context);
// Specialization of SortedEqualityCount with Comp = mgpu::less<T>.
template<typename InputIt1, typename InputIt2, typename InputIt3,
typename OutputIt, typename Op>
MGPU_HOST void SortedEqualityCount(InputIt1 a_global, int aCount,
InputIt2 b_global, int bCount, InputIt3 lb_global, OutputIt counts_global,
Op op, CudaContext& context);Searching data is a critical part of all computing systems. On the GPU, because of the extreme width of the processor, we need to be a bit creative to fully utilize the device while executing a search. The Thrust library includes vectorized binary searches in which all threads in the grid run their own independent binary search on sorted inputs. The user passes multiple "needles" (the keys you search for) and a sorted "haystack" (what you are looking in). Thousands of needles are required to fill the width of the machine.
Even when batching a large array of queries, performance will drag if the needles are unsorted—random access to the haystack results in many cache misses. GPU cache lines are 128 bytes, and if querying 4-byte data types, sustained throughput will only hit 3% of peak bandwidth.
This project focuses on functions that take one or more sorted inputs and emit a sorted output. Consider taking this requirement to vectorized binary searching: rather than accept the divergent memory accesses caused by queries on random needles, we could sort needles to keep the L2 cache hot. Instead of using 3% of each fetched cache line, we'd expect high re-use of cache lines between neighboring threads. The same embarrassingly-parallel vectorized search function achieves much higher throughput with better data organization. Searching for sorted needles in a haystack is a well-motivated problem. Consider joining two database tables—these are likely both sorted coming off disk, will need to be in sorted order to perform a sort-merge join, and want sorted results to return as a rowset.
The work presented in previous MGPU pages inspired a specific algorithmic optimization to this problem of vectorized searching. If the needles are sorted, the lower- or upper-bound results must also be sorted. That is, if a binary search for key1 returns index1, a search for key2 >= key1 must return index2 >= index1. In the sequential implementation, if we're searching for key2 having already computed the result for key1, we can improve performance slightly by searching the interval (index1, end) rather than (begin, end), since index2 cannot appear in (begin, index1).
There is a still stronger optimization: turn the binary search (O(A log B) complexity, where A is the needle array and B is the haystack) into a linear search (O(A + B) complexity). Starting with pointers A and B at the heads of the needle and haystack arrays, respectively:
If B (haystack) is less than A (needle), advance B. Because the elements in A are sorted, we aren't advancing B past any possible results for yet-to-be-encountered elements in A.
Otherwise, the B pointer is the result for the A query. Set results[A] = B and advance to the next query in A.
Sorted search for CPU from benchmarksortedsearch/benchmarksortedsearch.cu
// Return lower-bound of A into B.
template<MgpuBounds Bounds, typename T, typename Comp>
void CPUSortedSearch(const T* a, int aCount, const T* b, int bCount,
int* indices, Comp comp) {
int aIndex = 0, bIndex = 0;
while(aIndex < aCount) {
bool p;
if(bIndex >= bCount)
p = true;
else
p = (MgpuBoundsUpper == Bounds)?
comp(a[aIndex], b[bIndex]) :
!comp(b[bIndex], a[aIndex]);
if(p) indices[aIndex++] = bIndex;
else ++bIndex;
}
}This code is obviously more efficient than processing each needle as a binary search. But what we've gained in work-efficiency we may have lost in parallelism: binary searches are embarassingly parallel while this linear search code processes queries sequentially.
It's instructive to compare CPUSortedSearch with SerialMerge, the GPU function that powers MGPU's merge and mergesort:
template<int VT, bool RangeCheck, typename T, typename Comp>
MGPU_DEVICE void SerialMerge(const T* keys_shared, int aBegin, int aEnd,
int bBegin, int bEnd, T* results, int* indices, Comp comp) {
T aKey = keys_shared[aBegin];
T bKey = keys_shared[bBegin];
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool p;
if(RangeCheck)
p = (bBegin >= bEnd) || ((aBegin < aEnd) && !comp(bKey, aKey));
else
p = !comp(bKey, aKey);
results[i] = p ? aKey : bKey;
indices[i] = p ? aBegin : bBegin;
if(p) aKey = keys_shared[++aBegin];
else bKey = keys_shared[++bBegin];
}
__syncthreads();
}Although they have some differences, both routines check out-of-range pointers and set the predicate appropriately. If both pointers are in-range, keys are compared with the comparator object. For sorted search, if A (the needle) is smaller, the output is set and A is incremented; if B (the haystack) is smaller, B is incremented. For serial merge, if A is smaller, output is stored and A is incremented; if B is smaller, output is stored and B is incremented. The only material difference between these routines is how results are returned: the traversals over the input arrays are identical.
We parallelize the vectorized sorted search just like we do the merge. Coarse- and fine-grained scheduling and partitioning code is reused from MGPU Merge. However because we stream over A and B data but only emit A elements, we need an additional in-CTA pass to compact results.
There is a surprising and welcomed benefit from using a linear search, beyond just the improved work-efficiency: If we search for the lower-bound of A into B, we can also recover the upper-bound of B into A in the same pass. This is possible with linear search because we encounter every element from B; it does not hold with binary search.
Sorted search (2) for CPU from benchmarksortedsearch/benchmarksortedsearch.cu
// Return lower-bound of A into B and upper-bound of B into A.
template<typename T, typename Comp>
void CPUSortedSearch2(const T* a, int aCount, const T* b, int bCount,
int* aIndices, int* bIndices, Comp comp) {
int aIndex = 0, bIndex = 0;
while(aIndex < aCount || bIndex < bCount) {
bool p;
if(bIndex >= bCount) p = true;
else if(aIndex >= aCount) p = false;
else p = !comp(b[bIndex], a[aIndex]);
if(p) aIndices[aIndex++] = bIndex;
else bIndices[bIndex++] = aIndex;
}
}The inputs are traversed in the same order as in CPUSortedSearch (and in merge), but there is now an output on every iteration. This function looks very much like merge. We even lose the sense of 'needles' and 'haystack,' as the arrays are treated symmetrically. Scheduling and partioning the parallel version will be handled the same as merge. This is further evidence for the argument presented in the introduction and reiterated through these pages: we gain flexibility, clarity, and performance by separating partitioning/scheduling and work logic.
Sorted search (3) for CPU from benchmarksortedsearch/benchmarksortedsearch.cu
// Return lower-bound of A into B and set the high bit if A has a match in B.
// Return upper-bound of B into A and set the high bit if B has a match in A.
template<typename T, typename Comp>
void CPUSortedSearch3(const T* a, int aCount, const T* b, int bCount,
int* aIndices, int* bIndices, Comp comp) {
int aIndex = 0, bIndex = 0;
while(aIndex < aCount || bIndex < bCount) {
bool p;
if(bIndex >= bCount) p = true;
else if(aIndex >= aCount) p = false;
else p = !comp(b[bIndex], a[aIndex]);
if(p) {
// Compare the current key in A with the current key in B.
bool match = bIndex < bCount && !comp(a[aIndex], b[bIndex]);
aIndices[aIndex++] = bIndex + ((int)match<< 31);
} else {
// Compare the current key in B with the previous key in A.
bool match = aIndex && !comp(a[aIndex - 1], b[bIndex]);
bIndices[bIndex++] = aIndex + ((int)match<< 31);
}
}
}The second version of the sorted search is augmented with additional compares. It sets the most significant bit of the output index if the corresponding key in A or B has a match in the complementary array. We're supporting comparators (C++-style), so to test equality we must verify that both !(A < B) and !(B < A). Fortunately the state of the two pointers implies one half of the expression for both match tests.
Advancing A (lower-bound search): We know that B cannot be less than A (or else we would be advancing B!). We can test for equality simply by testing that A is not less than B: !comp(a[aIndex], b[bIndex]).
Advancing B (upper-bound search): The match in A (if there is one) must be the previous element in A, a[aIndex - 1]. However because we got to this point, we know that B is not less than the previous element in A: if it were, then when examining the previous A we would have advanced B rather than A, and we wouldn't be at this state. The expression !comp(a[aIndex - 1], b[bIndex]) is all that is needed to test equality.
Vectorized sorted search is a detailed and information-heavy function. That it runs nearly as fast as merge encourages its use in many situations. It has a pleasing symmetry with merge, and in fact we can re-implement merge using vectorized sorted search to produce indices and Bulk Insert to insert data at these indices.
Load-balancing search, an amazingly useful intra-CTA utility, is a straight-forward specialization of vectorized sorted search. We demonstate pairing vectorized sorted search with load-balancing search to implement relational joins in a later page.
include/kernels/sortedsearch.cuh
template<int NT, int VT, MgpuBounds Bounds, bool IndexA, bool MatchA,
bool IndexB, bool MatchB, typename InputIt1, typename InputIt2, typename T,
typename Comp>
MGPU_DEVICE int2 DeviceLoadSortedSearch(int4 range, InputIt1 a_global,
int aCount, InputIt2 b_global, int bCount, int tid, int block,
T* keys_shared, int* indices_shared, Comp comp) {
int a0 = range.x;
int a1 = range.y;
int b0 = range.z;
int b1 = range.w;
int aCount2 = a1 - a0;
int bCount2 = b1 - b0;
// For matching:
// If UpperBound
// MatchA requires preceding B
// MatchB requires trailing A
// If LowerBound
// MatchA requires trailing B
// MatchB requires preceding A
int leftA = MatchB && (MgpuBoundsLower == Bounds) && (a0 > 0);
int leftB = MatchA && (MgpuBoundsUpper == Bounds) && (b0 > 0);
int rightA = a1 < aCount;
int rightB = b1 < bCount;
int aStart = leftA;
int aEnd = aStart + aCount2 + rightA;
int bStart = aEnd + leftB;
int bEnd = bStart + bCount2 + rightB;
// Cooperatively load all the data including halos.
DeviceLoad2ToShared<NT, VT, VT + 1>(a_global + a0 - leftA, aEnd,
b_global + b0 - leftB, bEnd - aEnd, tid, keys_shared);
// Run the serial searches and compact the indices into shared memory.
bool extended = rightA && rightB && (!MatchA || leftB) &&
(!MatchB || leftA);
int2 matchCount = CTASortedSearch<NT, VT, Bounds, IndexA, MatchA, IndexB,
MatchB>(keys_shared, aStart, aCount2, aEnd, a0, bStart, bCount2, bEnd,
b0, extended, tid, indices_shared, comp);
return matchCount;
}One vectorized sorted search kernel supports many modes of operation. The host function that launches KernelSortedSearch separates the MgpuSearchType enums into individual flags for IndexA, MatchA, IndexB, and MatchB. The kernel calls DeviceLoadSortedSearch which loads the intervals from the A and B arrays, runs a MergePath search on each thread, and performs a serial search over VT inputs per thread.
Different modes have different requirements:
| Lower-bound | Upper-bound | |
| MatchA | trailing B | preceding B |
| MatchB | preceding A | trailing A |
Merge Path partitioning divides A and B inputs into distinct, non-overlapping intervals. Loading just these intervals into a tile's shared memory is insufficient to support match operations. For a lower-bound search, equal elements are consumed from A before B. If an element A[i] has a match in B at B[j], B[j] will appear after A[i] in the Merge Path. The thread checking the match of A[i] needs access to B[j], even if B[j] is mapped to a subsequent tile.
The search types are decomposed and the interval pointers incremented or decremented to accommodate the extra terms requried to verify matches. DeviceLoad2ToShared cooperatively loads intervals from two source arrays and stores to shared memory. It incorporates an optimization to handle extended cases like this: for a nominal tile (i.e. all tiles except the partial tile at the end) each thread loads VT items—these VT loads are included in an unpredicated form, written to encourage maximum outstanding loads and reduce latency. At most the kernel loads only four additional items beyond this (one each for the preceding and trailing items from A and B), and only this final load is predicated. In other words: DeviceLoad2ToShared<NT, VT, VT + 1> generates an optimized path for full tiles, in which the first VT loads are unpredicated and the last load is predicated.
If a "halo" element has been loaded after the last A and B inputs, the extended flag is set and we omit range checks in the serial search code. CTASortedSearch computes search indices and matches into shared memory and returns match counts (of both A into B and B into A) to the caller. The calling function, KernelSortedSearch, copies the indices and match flags out of shared memory and into their respective output arrays.
include/device/ctasortedsearch.cuh
template<int NT, int VT, MgpuBounds Bounds, bool IndexA, bool MatchA,
bool IndexB, bool MatchB, typename T, typename Comp>
MGPU_DEVICE int2 CTASortedSearch(T* keys_shared, int aStart, int aCount,
int aEnd, int a0, int bStart, int bCount, int bEnd, int b0, bool extended,
int tid, int* indices_shared, Comp comp) {
// Run a merge path to find the start of the serial search for each thread.
int diag = VT * tid;
int mp = MergePath<Bounds>(keys_shared + aStart, aCount,
keys_shared + bStart, bCount, diag, comp);
int a0tid = mp;
int b0tid = diag - mp;
// Serial search into register.
int3 results;
int indices[VT];
if(extended)
results = DeviceSerialSearch<VT, Bounds, false, IndexA, MatchA, IndexB,
MatchB>(keys_shared, a0tid + aStart, aEnd, b0tid + bStart, bEnd,
a0 - aStart, b0 - bStart, indices, comp);
else
results = DeviceSerialSearch<VT, Bounds, true, IndexA, MatchA, IndexB,
MatchB>(keys_shared, a0tid + aStart, aEnd, b0tid + bStart, bEnd,
a0 - aStart, b0 - bStart, indices, comp);
__syncthreads();
// Compact the indices into shared memory. Use the decision bits (set is A,
// cleared is B) to select the destination.
int decisions = results.x;
b0tid += aCount;
#pragma unroll
for(int i = 0; i < VT; ++i) {
if((1<< i) & decisions) {
if(IndexA || MatchA) indices_shared[a0tid++] = indices[i];
} else {
if(IndexB || MatchB) indices_shared[b0tid++] = indices[i];
}
}
__syncthreads();
// Return the match counts for A and B keys.
return make_int2(results.y, results.z);
}CTASortedSearch follows the same recipe that makes MGPU Merge (and Mergesort and Segmented Sort) so efficient, but adds a few twists:
The host function calls MergePathPartitions to globally partition the input arrays into tile-sized chunks, as in merge.
In the sorted search kernel, data is cooperatively loaded from A and B arrays into shared memory.
Each thread runs a MergePath search for every VT * tid cross-diagonal.
DeviceSerialSearch is invoked with the offsets from 3. Each thread traverses VT elements in an unrolled loop and computes search results. Search indices/matches are returned in the order in which they are encountered. The set of decision bits are returned in order in results.x.
After synchronization, each thread steps through its VT indices and distributes them to either the A or B output arrays.
The number of A matches in B and B matches in A are returned to the caller, which may then use CTAReduce to find a total within the tile, and atomically increment the global match counters.
include/device/ctasortedsearch.cuh
template<int VT, MgpuBounds Bounds, bool RangeCheck, bool IndexA, bool MatchA,
bool IndexB, bool MatchB, typename T, typename Comp>
MGPU_DEVICE int3 DeviceSerialSearch(const T* keys_shared, int aBegin,
int aEnd, int bBegin, int bEnd, int aOffset, int bOffset, int* indices,
Comp comp) {
const int FlagA = IndexA ? 0x80000000 : 1;
const int FlagB = IndexB ? 0x80000000 : 1;
T aKey = keys_shared[aBegin];
T bKey = keys_shared[bBegin];
T aPrev, bPrev;
if(aBegin > 0) aPrev = keys_shared[aBegin - 1];
if(bBegin > 0) bPrev = keys_shared[bBegin - 1];
int decisions = 0;
int matchCountA = 0;
int matchCountB = 0;
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool p;
if(RangeCheck && aBegin >= aEnd) p = false;
else if(RangeCheck && bBegin >= bEnd) p = true;
else p = (MgpuBoundsUpper == Bounds) ?
comp(aKey, bKey) :
!comp(bKey, aKey);
if(p) {
// aKey is smaller than bKey, so it is inserted before bKey.
// Save bKey's index (bBegin + first) as the result of the search
// and advance to the next needle in A.
bool match = false;
if(MatchA) {
// Test if there is an element in B that matches aKey.
if(MgpuBoundsUpper == Bounds) {
bool inRange = !RangeCheck || (bBegin > aEnd);
match = inRange && !comp(bPrev, aKey);
} else {
bool inRange = !RangeCheck || (bBegin < bEnd);
match = inRange && !comp(aKey, bKey);
}
}
int index = 0;
if(IndexA) index = bOffset + bBegin;
if(match) index |= FlagA;
if(IndexA || MatchA) indices[i] = index;
matchCountA += match;
// Mark the decision bit to indicate that this iteration has
// progressed A (the needles).
decisions |= 1<< i;
aPrev = aKey;
aKey = keys_shared[++aBegin];
} else {
// aKey is larger than bKey, so it is inserted after bKey (but we
// don't know where yet). Advance the B index to the next element in
// the haystack to continue the search for the current needle.
bool match = false;
if(MatchB) {
if(MgpuBoundsUpper == Bounds) {
bool inRange = !RangeCheck ||
((bBegin < bEnd) && (aBegin < aEnd));
match = inRange && !comp(bKey, aKey);
} else {
bool inRange = !RangeCheck ||
((bBegin < bEnd) && (aBegin > 0));
match = inRange && !comp(aPrev, bKey);
}
}
int index = 0;
if(IndexB) index = aOffset + aBegin;
if(match) index |= FlagB;
if(IndexB || MatchB) indices[i] = index;
matchCountB += match;
// Keep the decision bit cleared to indicate that this iteration
// has progressed B (the haystack).
bPrev = bKey;
bKey = keys_shared[++bBegin];
}
}
return make_int3(decisions, matchCountA, matchCountB);
}DeviceSerialSearch is a massive function that services the many permutations that vectorized sorted search supports. Search results are stored directly into the indices register array and are redistributed into shared memory by CTASortedSearch. Rather than having to provision space for both the source and destination in shared memory, halving occupancy, we provision only enough for the source data—outputs are produced into register; the CTA is synchronized; and the results are stored back to the same shared memory array.
When run on full tiles, DeviceSerialSearch is specialized with RangeCheck = false (corresponding to extended = true in CTASortedSearch), allowing it to elide range-checking logic that adds significant latency to execution. This is an optimization that can be made for merge, mergesort, and segmented mergesort as well. However, it has been prioritized here because A) there's potentially much more logic here to contend with; and B) DeviceLoadSortedSearch already is loading in halo elements to support match operations, so adding a specialization to elide range checks took minimal effort.
While reviewing the logic for the four match tests, keep in mind that equality is established with two less-than checks: !(aKey < bKey) && !(bKey < aKey); or when written with comparators: !comp(aKey, bKey) && !comp(bKey, aKey).
When computing the lower-bound of A into B (and the upper-bound of B into A);
To match A (p = true): We're inserting aKey before bKey. If there is a match for aKey it must be bKey. Check that bKey is in range and equal to aKey. Half of the equality test has already been computed when we made the predicate test !comp(bKey, aKey). Check the other half of the equality condition with a second comparison: !comp(aKey, bKey).
To match B (p = false): The predicate test has confirmed that bKey is smaller than aKey (comp(bKey, aKey) is true). If there is a match for bKey it must be aPrev. The previous A-advancing iteration proved that !comp(bKey, aPrev). Check the other half of the equality condition with a second comparison: !comp(aPrev, bKey).
When computing the upper-bound of A into B (and the lower-bound of B into A) we flip the arguments around:
To match A (p = true): We're inserting aKey after bKey. If there is a match for aKey it must be bPrev. Check that bPrev is in range and equal to aKey. The previous A-advancing iteration proved that !comp(aKey, bPrev); it failed the comp(aKey, bKey) test and advanced B to get us to this point. Check the other half of the equality condition with a second comparison: !comp(bPrev, aKey).
To match B (p = false): The predicate test has confirmed that aKey is not smaller than bKey. If there is a match for bKey it must be aKey. Check the other half of the equality condition with a second comparison: !comp(bKey, aKey).
Vectorized sorted search is a powerful merge-like function. It's put to good use when implementing relational joins. More importantly, it motivates the useful and elegant load-balancing search, the subject of the next page.
include/kernels/sortedsearch.cuh
struct SortedEqualityOp {
MGPU_HOST_DEVICE int operator()(int lb, int ub) const {
return ub - lb;
}
};
template<typename Tuning, typename InputIt1, typename InputIt2,
typename InputIt3, typename OutputIt, typename Comp, typename Op>
MGPU_LAUNCH_BOUNDS void KernelSortedEqualityCount(InputIt1 a_global, int aCount,
InputIt2 b_global, int bCount, const int* mp_global, InputIt3 lb_global,
OutputIt counts_global, Comp comp, Op op) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
union Shared {
int keys[NT * (VT + 1)];
int indices[NV];
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int4 range = ComputeMergeRange(aCount, bCount, block, 0, NV, mp_global);
// Compute the upper bound.
int2 matchCount = DeviceLoadSortedSearch<NT, VT, MgpuBoundsUpper, true,
false, false, false>(range, a_global, aCount, b_global, bCount, tid,
block, shared.keys, shared.indices, comp);
int aCount2 = range.y - range.x;
// Load the lower bounds computed by the previous launch.
int lb[VT];
DeviceGlobalToReg<NT, VT>(aCount2, lb_global + range.x, tid, lb);
// Subtract the lower bound from the upper bound and store the count.
counts_global += range.x;
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = NT * i + tid;
if(index < aCount2) {
int count = op(lb[i], shared.indices[index]);
counts_global[index] = count;
}
}
}C++ standard library functions std::equal_range binary searches for a single key in an array and returns the pair of (lower-bound, upper-bound) iterators. std::count runs a similar search but returns the count of occurrences, which is equal to the difference of the upper- and lower-bounds.
Vectorized sorted search doesn't extend naturally to support equal-range queries in a single pass because partitioning and scheduling decisions are made specifically for either lower- or upper-bound duplicate semantics. We can, at least, provide a modest optimization for achieving a vectorized count function. Rather than running lower- and upper-bound searches independently and launching a third kernel to take differences, we've provided a SortedSearch specialization that finds upper-bound indices of A into B, then loads lower-bound indices that correspond to each output and computes and stores counts directly.
SortedEqualityCount is specialized over a user-provided difference operator. This adds flexibility to the function, allowing it to extract index bits of a match-decorated sorted search result, or to max the difference with a constant. (It's this usage that enables our relational left-join function.)