
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
A high-throughput mergesort that is perfectly load-balanced over all threads. Develops partitioning and scheduling functions that are used throughout these pages. This mergesort is the basis for high-performance segmented and locality sorts that work with structured data (i.e. non-uniformly random).

Sort Keys benchmark from benchmarksort/benchmarksort.cu
Sort keys demonstration from tests/demo.cu
void DemoSortKeys(CudaContext& context) {
printf("\n\nSORT KEYS DEMONSTRATION:\n\n");
// Use CudaContext::GenRandom to generate 100 random integers between 0 and
// 199.
int N = 100;
MGPU_MEM(int) data = context.GenRandom<int>(N, 0, 99);
printf("Input:\n");
PrintArray(*data, "%4d", 10);
// Mergesort keys.
MergesortKeys(data->get(), N, mgpu::less<int>(), context);
printf("\nSorted output:\n");
PrintArray(*data, "%4d", 10);
}SORT KEYS DEMONSTRATION:
Input:
0: 5 95 68 53 4 87 7 93 52 66
10: 9 28 81 6 81 23 72 70 14 19
20: 65 42 51 93 97 14 64 64 80 47
30: 45 43 43 24 82 50 8 90 13 7
40: 17 71 39 61 83 18 80 39 6 27
50: 39 85 52 90 41 61 65 18 62 51
60: 29 82 43 35 1 81 98 29 16 17
70: 10 49 37 19 19 86 48 20 33 61
80: 95 87 92 39 5 94 73 16 26 97
90: 42 56 54 59 94 13 41 56 98 55
Sorted output:
0: 1 4 5 5 6 6 7 7 8 9
10: 10 13 13 14 14 16 16 17 17 18
20: 18 19 19 19 20 23 24 26 27 28
30: 29 29 33 35 37 39 39 39 39 41
40: 41 42 42 43 43 43 45 47 48 49
50: 50 51 51 52 52 53 54 55 56 56
60: 59 61 61 61 62 64 64 65 65 66
70: 68 70 71 72 73 80 80 81 81 81
80: 82 82 83 85 86 87 87 90 90 92
90: 93 93 94 94 95 95 97 97 98 98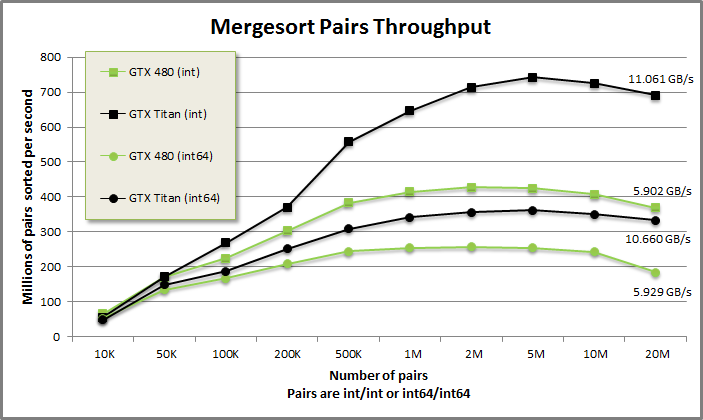
Sort Pairs benchmark from benchmarksort/benchmarksort.cu
Sort pairs demonstration from tests/demo.cu
void DemoSortPairs(CudaContext& context) {
printf("\n\nSORT PAIRS DEMONSTRATION:\n\n");
// Use CudaContext::GenRandom to generate 100 random integers between 0 and
// 99.
int N = 100;
MGPU_MEM(int) keys = context.GenRandom<int>(N, 0, 99);
MGPU_MEM(int) vals = context.FillAscending<int>(N, 0, 1);
printf("Input keys:\n");
PrintArray(*keys, "%4d", 10);
// Mergesort pairs.
MergesortPairs(keys->get(), vals->get(), N, mgpu::less<int>(), context);
printf("\nSorted keys:\n");
PrintArray(*keys, "%4d", 10);
printf("\nSorted values:\n");
PrintArray(*vals, "%4d", 10);
}Input:
0: 30 31 70 12 66 73 53 24 69 82
10: 66 18 17 31 12 88 99 67 17 73
20: 3 6 56 13 88 8 66 0 19 45
30: 36 63 46 52 98 49 15 33 85 25
40: 64 23 37 17 19 59 42 72 48 87
50: 12 70 58 23 22 47 38 1 58 74
60: 25 65 29 7 61 47 26 99 82 53
70: 98 89 73 77 34 20 58 90 10 37
80: 90 84 87 32 81 32 26 65 59 58
90: 2 4 42 76 31 49 16 48 17 42
Sorted keys:
0: 0 1 2 3 4 6 7 8 10 12
10: 12 12 13 15 16 17 17 17 17 18
20: 19 19 20 22 23 23 24 25 25 26
30: 26 29 30 31 31 31 32 32 33 34
40: 36 37 37 38 42 42 42 45 46 47
50: 47 48 48 49 49 52 53 53 56 58
60: 58 58 58 59 59 61 63 64 65 65
70: 66 66 66 67 69 70 70 72 73 73
80: 73 74 76 77 81 82 82 84 85 87
90: 87 88 88 89 90 90 98 98 99 99
Sorted values:
0: 27 57 90 20 91 21 63 25 78 3
10: 14 50 23 36 96 12 18 43 98 11
20: 28 44 75 54 41 53 7 39 60 66
30: 86 62 0 1 13 94 83 85 37 74
40: 30 42 79 56 46 92 99 29 32 55
50: 65 48 97 35 95 33 6 69 22 52
60: 58 76 89 45 88 64 31 40 61 87
70: 4 10 26 17 8 2 51 47 5 19
80: 72 59 93 73 84 9 68 81 38 49
90: 82 15 24 71 77 80 34 70 16 67//////////////////////////////////////////////////////////////////////////////// // kernels/mergesort.cuh // MergesortKeys sorts data_global using comparator Comp. // If !comp(b, a), then a comes before b in the output. The data is sorted // in-place. template<typename T, typename Comp> MGPU_HOST void MergesortKeys(T* data_global, int count, Comp comp, CudaContext& context); // MergesortKeys specialized with Comp = mgpu::less<T>. template<typename T> MGPU_HOST void MergesortKeys(T* data_global, int count, CudaContext& context); // MergesortPairs sorts data by key, copying data. This corresponds to // sort_by_key in Thrust. template<typename KeyType, typename ValType, typename Comp> MGPU_HOST void MergesortPairs(KeyType* keys_global, ValType* values_global, int count, Comp comp, CudaContext& context); // MergesortPairs specialized with Comp = mgpu::less<KeyType>. template<typename KeyType, typename ValType> MGPU_HOST void MergesortPairs(KeyType* keys_global, ValType* values_global, int count, CudaContext& context); // MergesortIndices is like MergesortPairs where values_global is treated as // if initialized with integers (0 ... count - 1). template<typename KeyType, typename Comp> MGPU_HOST void MergesortIndices(KeyType* keys_global, int* values_global, int count, Comp comp, CudaContext& context); // MergesortIndices specialized with Comp = mgpu::less<KeyType>. template<typename KeyType> MGPU_HOST void MergesortIndices(KeyType* keys_global, int* values_global, int count, CudaContext& context);
Mergesort recursively merges sorted lists until the sequence is fully sorted.
Input array is treated as sequence of sorted lists of length 1: 13 90 83 12 96 91 22 63 30 9 54 27 18 54 99 95 Merge adjacent pairs of length-1 lists into sequence of length-2 lists: 13 90 12 83 91 96 22 63 9 30 27 54 18 54 95 99 Merge adjacent pairs of length-2 lists into sequence of length-4 lists: 12 13 83 90 22 63 91 96 9 27 30 54 18 54 95 99 Merge adjacent pairs of length-4 lists into sequence of length-8 lists: 12 13 22 63 83 90 91 96 9 18 27 30 54 54 95 99 Merge adjacent pairs of length-8 lists into final length-16 output: 9 12 13 18 22 27 30 54 54 63 83 90 91 95 96 99
Although mergesort takes one unsorted array as in input, thematically it is the same as the functions that make up the bulk of MGPU: take two sorted inputs and emit one sorted output. This is clear if treat consecutive input elements as two sorted lists of length 1. Mergesort is type of multi-pass vectorized merge: the first iteration executes N / 2 merges with inputs of length 1; the second iteration executes N / 4 merges with inputs of length 2; etc.
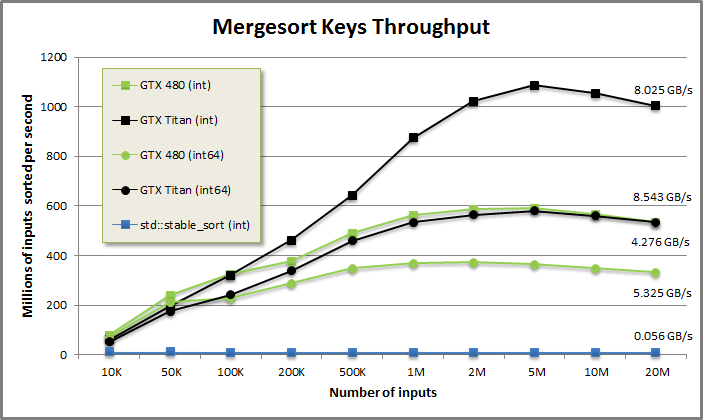
The number of batched merge passes is log(N) and the work per pass is N. This O(N log N) work-efficiency hurts mergesort's scalability compared to radix sort. This mergesort implementation runs at about half the throughput on large arrays with 32-bit keys as the fastest GPU radix sorts. But it still clocks about 100x faster than calling std::stable_sort on an i7 Sandy Bridge. If the sort is truly on a critical path, it may be worth pulling a radix sort from B40C/FastSortSm20. Otherwise you can get by just fine with this very hackable mergesort, or use one of MGPU's higher-performance derivative sorts (segmented sort or locality sort).
O(N log N) complexity aside, mergesort has some notable advantages over radix sort:
Mergesort is a comparison sort. While radix sort requires types to have the same lexicographical order as integers, limiting practical use to numeric types like ints and floats, mergesort accepts a user-defined comparator function. This allows mergesort to efficiently handle types like strings by calling strcmp from the comparator.
Mergesort scales better as keys get larger. Radix sort's work-efficiency is O(k N), where k is the key size in bits. Mergesort's complexity is only dependent on the number of input elements.
Mergesort provides extremely fast CTA-level blocksorts. On small inputs (like data mapped into an individual tile) the O(log N) penalty is on order with radix sort's O(k) penalty. Mergesort's simpler, faster inner loop allows blocksorts that are more flexible, easier to maintain, and often quicker than radix blocksorts.
Mergesort makes data progressively more sorted, never less. Even when launched on fully-sorted inputs, LSB radix sort randomly scatters data each pass, only putting the data into sorted order during the final pass. On fully sorted inputs, mergesort simply copies the data log(N) times. This pass-to-pass coherence allows detection of sorted intervals and early-exits to reduce unnecessary work. The O(N log N) complexity is only for uniform random inputs—data with exploitable structure can be sorted with far fewer comparisons. The next page builds special-case mergesorts that detect input structure and early-exit out of unnecessary operations.
Mergesort on GPU runs best when written in two distinct stages:
A blocksort kernel sorts random inputs into tile-length sorted lists, communicating with low-latency, high-bandwidth shared memory .The CTA blocksort forms a convenient re-usable component for MGPU's customers.
Multiple launches of MGPU Merge iteratively merge sorted lists, starting with the output of 1, communicating between passes with high-latency, high-capacity DRAM.
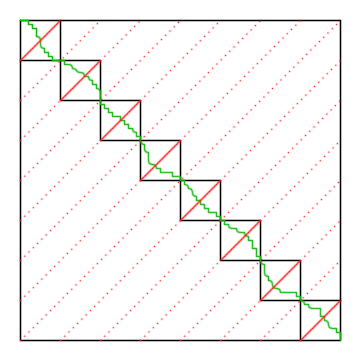
Mergesort merge pass with coop = 2
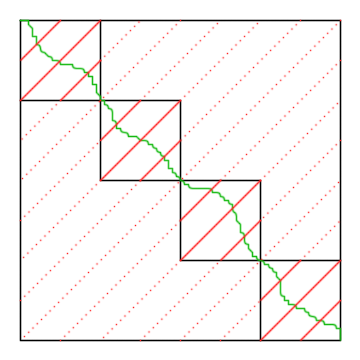
Mergesort merge pass with coop = 4
Both the blocksort and global merge passes follow the structure illustrated above. Pairs of threads (or CTAs for the global merge passes) cooperatively merge two VT-length lists (or two NV-length lists) into one list. This phase is noted coop = 2, for 2 threads cooperating on each pair of input lists. During the coop = 4 pass, 4 threads cooperatively merge two lists into one; during coop = 8, 8 threads cooperatively merge two lists; and so on. Although there are many sorted lists in the data, threads cooperatively merge from only two of them at a time.
The figure at the top shows 16 sorted lists (each segment along the top and right of a square is a list). Two threads cooperate to merge each pair of lists (a square) into a single list (a segment) for the coop = 4 pass. Threads 0 and 1 merge the top and right segments of the first pair in coop = 2 into the top segment of the first pair in coop = 4; threads 2 and 3 merge the top and right segments of the second pair in coop = 2 into the right segment of the first pair in coop = 4; etc. This process continues until only a single sorted list remains.
For each global merge pass, a call to MergePathPartitions partitions the input arrays into tile-sized chunks. ComputeMergeRange is invoked early in KernelMerge to identify the intervals of the input to load. We then hand the intra-CTA merging to DeviceMerge, developed in the previous page.
MGPU's blocksort loads VT values per thread over NT threads per CTA. Merging requires dynamic indexing, which means shared memory. The first few rounds of merges can be replaced by an in-register sorting network. Batcher's odd-even mergesort sorts inputs in O(n log2 n time) using only comparisons and swaps. The odd-even transposition sort takes O(n2) comparisons but adds stability. These sorting networks are relatively inefficient, but expose great amounts of immediate parallelism, making them effective tools for sorting small inputs.
Although MGPU includes an implementation for Batcher's odd-even mergesort (in sortnetwork.cuh), the slower odd-even transposition sort is preferred, because it is stable. It takes more comparisons to sort a thread using this network, but the cost is small compared to the cost of the many recursive merge passes that follow.
13 90 83 12 96 91 22 63 30 9 54 27 18 54 99 95 (13 90) (12 83) (91 96) (22 63) ( 9 30) (27 54) (18 54) (95 99) (12 90) (83 91) (22 96) ( 9 63) (27 30) (18 54) (54 95) (12 13) (83 90) (22 91) ( 9 96) (27 63) (18 30) (54 54) (95 99) (13 83) (22 90) ( 9 91) (27 96) (18 63) (30 54) (54 95) (12 13) (22 83) ( 9 90) (27 91) (18 96) (30 63) (54 54) (95 99) (13 22) ( 9 83) (27 90) (18 91) (30 96) (54 63) (54 95) (12 13) ( 9 22) (27 83) (18 90) (30 91) (54 96) (54 63) (95 99) ( 9 13) (22 27) (18 83) (30 90) (54 91) (54 96) (63 95) ( 9 12) (13 22) (18 27) (30 83) (54 90) (54 91) (63 96) (95 99) (12 13) (18 22) (27 30) (54 83) (54 90) (63 91) (95 96) ( 9 12) (13 18) (22 27) (30 54) (54 83) (63 90) (91 95) (96 99) (12 13) (18 22) (27 30) (54 54) (63 83) (90 91) (95 96) ( 9 12) (13 18) (22 27) (30 54) (54 63) (83 90) (91 95) (96 99) (12 13) (18 22) (27 30) (54 54) (63 83) (90 91) (95 96) ( 9 12) (13 18) (22 27) (30 54) (54 63) (83 90) (91 95) (96 99) (12 13) (18 22) (27 30) (54 54) (63 83) (90 91) (95 96) 9 12 13 18 22 27 30 54 54 63 83 90 91 95 96 99
Sorting an array of N inputs needs N transposition passes. Stability is gained by only comparing pairs of neighboring elements, and only exchanging when the element on the right is smaller. 16 inputs are sorted in this illustration. Pairs starting at offset 0 are compared and swapped on even passes; pairs starting at offset 1 are compared and swapped on odd passes. Items in the same pair are drawn in the same color - observe that the second pair of values (83, 12) are swapped into (12, 83) during the first pass. The small 9 that starts in the middle is moved peristaltically to the front of the array.
We get the problem started by loading and transposing VT elements per thread into register, so that each thread has items VT * tid + i in register. Each thread calls OddEvenTransposeSort to sort its own set of elements in register. This phase of the blocksort uses no shared memory and has high ILP (all of the compare-and-swaps in each row can be performed in parallel).
include/device/sortnetwork.cuh
template<int VT, typename T, typename V, typename Comp>
MGPU_DEVICE void OddEvenTransposeSort(T* keys, V* values, Comp comp) {
#pragma unroll
for(int level = 0; level < VT; ++level) {
#pragma unroll
for(int i = 1 & level; i < VT - 1; i += 2) {
if(comp(keys[i + 1], keys[i])) {
mgpu::swap(keys[i], keys[i + 1]);
mgpu::swap(values[i], values[i + 1]);
}
}
}
}Odd-even transposition sort has two nested loops: the outer iterates over the number of inputs (each row in the figure); the inner iterates over the number of pairs, as shown above. Unfortunately CUDA's #pragma unroll feature still has some kinks, and the compiler currently fails to unroll all the static indexing when the function is written this way. Spills result.
include/device/sortnetwork.cuh
template<int I, int VT>
struct OddEvenTransposeSortT {
// Sort segments marked by head flags. If the head flag between i and i + 1
// is set (so that (2<< i) & flags is true), the values belong to different
// segments and are not swapped.
template<typename K, typename V, typename Comp>
static MGPU_DEVICE void Sort(K* keys, V* values, int flags,
Comp comp) {
#pragma unroll
for(int i = 1 & I; i < VT - 1; i += 2)
if((0 == ((2<< i) & flags)) && comp(keys[i + 1], keys[i])) {
mgpu::swap(keys[i], keys[i + 1]);
mgpu::swap(values[i], values[i + 1]);
}
OddEvenTransposeSortT<I + 1, VT>::Sort(keys, values, flags, comp);
}
};
template<int I> struct OddEvenTransposeSortT<I, I> {
template<typename K, typename V, typename Comp>
static MGPU_DEVICE void Sort(K* keys, V* values, int flags,
Comp comp) { }
};
template<int VT, typename K, typename V, typename Comp>
MGPU_DEVICE void OddEvenTransposeSort(K* keys, V* values, Comp comp) {
OddEvenTransposeSortT<0, VT>::Sort(keys, values, 0, comp);
}
template<int VT, typename K, typename V, typename Comp>
MGPU_DEVICE void OddEvenTransposeSortFlags(K* keys, V* values, int flags,
Comp comp) {
OddEvenTransposeSortT<0, VT>::Sort(keys, values, flags, comp);
}We bend to pragmatism and write the code like this. Template loop unrolling replaces the #pragma unroll nesting, allowing the sorting network to compile correctly. This implementation takes a bitfield of segment head flags to support the segmented sort (we'll revisit this part on the next page). For standard mergesort, the bitfield is always 0 and the associated logic is eliminated by the compiler.
template<int NT, int VT, bool HasValues, typename KeyType, typename ValType,
typename Comp>
MGPU_DEVICE void CTAMergesort(KeyType threadKeys[VT], ValType threadValues[VT],
KeyType* keys_shared, ValType* values_shared, int count, int tid,
Comp comp) {
// Stable sort the keys in the thread.
if(VT * tid < count)
OddEvenTransposeSort<VT>(threadKeys, threadValues, comp);
// Store the locally sorted keys into shared memory.
DeviceThreadToShared<VT>(threadKeys, tid, keys_shared);
// Recursively merge lists until the entire CTA is sorted.
DeviceBlocksortLoop<NT, VT, HasValues>(threadValues, keys_shared,
values_shared, tid, count, comp);
}CTAMergesort is a reusable block-level mergesort. MGPU uses this function for the locality sort function in addition to standard mergesort. If the user wants to only sort keys, set HasValues to false and ValType to int. Use this function by passing unsorted keys and values in thread order (i.e. VT * tid + i) through register. On return, the same register arrays contain fully-sorted data. Shared memory is also filled with the sorted keys, making coalesced stores back to global memory convenient.
When sorting a partial tile, pad out the last valid thread (the last thread in the CTA with with in-range values) with copies of the largest key in that thread. The actual mergesort can handle partial blocks just fine: this padding helps keep the sorting network simple. (We only specialize the sorting network for one size, VT.)
After running the intra-thread sorting network we need to recursively merge sorted lists. Start with pairs of threads cooperating on one destination. Call this pass coop = 2, because two threads cooperate on each output list. As the list size doubles, so does the number of cooperating threads per list. We loop until only a single sorted list remains.
template<int NT, int VT, bool HasValues, typename KeyType, typename ValType,
typename Comp>
MGPU_DEVICE void CTABlocksortLoop(ValType threadValues[VT],
KeyType* keys_shared, ValType* values_shared, int tid, int count,
Comp comp) {
#pragma unroll
for(int coop = 2; coop <= NT; coop *= 2) {
int indices[VT];
KeyType keys[VT];
CTABlocksortPass<NT, VT>(keys_shared, tid, count, coop, keys,
indices, comp);
if(HasValues) {
// Exchange the values through shared memory.
DeviceThreadToShared<VT>(threadValues, tid, values_shared);
DeviceGather<NT, VT>(NT * VT, values_shared, indices, tid,
threadValues);
}
// Store results in shared memory in sorted order.
DeviceThreadToShared<VT>(keys, tid, keys_shared);
}
}CTABlocksortLoop is called with keys sorted into VT-length lists in shared memory. Values are passed in thread order in register (threadValues). Log(NT) loop iterations are made. CTABlocksortPass returns merged keys and indices in register. With the merged keys in safely in register, the function writes back the new lists with DDeviceThreadToShared. It gathers them back into register with DeviceGather.
Note that we only have the input or output data staged in shared memory at any one time, not both. MGPU Mergesort is fast because it intelligently manages occupancy this way.
template<int NT, int VT, typename T, typename Comp>
MGPU_DEVICE void CTABlocksortPass(T* keys_shared, int tid,
int count, int coop, T* keys, int* indices, Comp comp) {
int list = ~(coop - 1) & tid;
int diag = min(count, VT * ((coop - 1) & tid));
int start = VT * list;
int a0 = min(count, start);
int b0 = min(count, start + VT * (coop / 2));
int b1 = min(count, start + VT * coop);
int p = MergePath<MgpuBoundsLower>(keys_shared + a0, b0 - a0,
keys_shared + b0, b1 - b0, diag, comp);
SerialMerge<VT, true>(keys_shared, a0 + p, b0, b0 + diag - p, b1, keys,
indices, comp);
}Locating each thread's pair of source lists, destination list, and position within the output is the first task of the vectorized merge function CTABlocksortPass. ~(coop - 1) & tid masks out the bits that position each thread's cross-diagonal within the destination list. This expression serves as a scaled destination list index and is mulitplied by VT to target the start of the A list in shared memory. The expression VT * ((coop - 1) & tid) locates each thread's cross-diagonal in the local coordinate system of the output list.
NT = 8, VT = 7, count = 49 (full tile) tid coop = 2 coop = 4 coop = 8 0: A=( 0, 7),B=( 7, 14),d= 0 A=( 0, 14),B=(14, 28),d= 0 A=( 0, 28),B=(28, 56),d= 0 1: A=( 0, 7),B=( 7, 14),d= 7 A=( 0, 14),B=(14, 28),d= 7 A=( 0, 28),B=(28, 56),d= 7 2: A=(14, 21),B=(21, 28),d= 0 A=( 0, 14),B=(14, 28),d=14 A=( 0, 28),B=(28, 56),d=14 3: A=(14, 21),B=(21, 28),d= 7 A=( 0, 14),B=(14, 28),d=21 A=( 0, 28),B=(28, 56),d=21 4: A=(28, 35),B=(35, 42),d= 0 A=(28, 42),B=(42, 56),d= 0 A=( 0, 28),B=(28, 56),d=28 5: A=(28, 35),B=(35, 42),d= 7 A=(28, 42),B=(42, 56),d= 7 A=( 0, 28),B=(28, 56),d=35 6: A=(42, 49),B=(49, 56),d= 0 A=(28, 42),B=(42, 56),d=14 A=( 0, 28),B=(28, 56),d=42 7: A=(42, 49),B=(49, 56),d= 7 A=(28, 42),B=(42, 56),d=21 A=( 0, 28),B=(28, 56),d=49
These intervals illustrate all blocksort passes for a full tile with 8 threads and 7 values per thread. You can work them out using the bit-twiddling described above. The length of the cross-diagonal in a Merge Path search is constrained by the length of the shorter of the two input arrays. The cross-diagonal length doubles each iteration: 7, 14, 28... Correspondingly the depth (and cost) of the binary search increments as we progress in the mergesort: 3, 4, 5... This simple iterative approach to blocksort perfectly load balances scheduling and merging work over the CTA.
After the blocksort we have NV-length lists sorted in global memory. We recursively run a merge on pairs of lists until the entire array is sorted. Just like the CTA mergesort uses code from our CTA-level merge, the global mergesort uses code from the global merge.
// Returns (offset of a, offset of b, length of list).
MGPU_HOST_DEVICE int3 FindMergesortFrame(int coop, int block, int nv) {
// coop is the number of CTAs or threads cooperating to merge two lists into
// one. We round block down to the first CTA's ID that is working on this
// merge.
int start = ~(coop - 1) & block;
int size = nv * (coop>> 1);
return make_int3(nv * start, nv * start + size, size);
}
// Returns (a0, a1, b0, b1) into mergesort input lists between mp0 and mp1.
MGPU_HOST_DEVICE int4 FindMergesortInterval(int3 frame, int coop, int block,
int nv, int count, int mp0, int mp1) {
// Locate diag from the start of the A sublist.
int diag = nv * block - frame.x;
int a0 = frame.x + mp0;
int a1 = min(count, frame.x + mp1);
int b0 = min(count, frame.y + diag - mp0);
int b1 = min(count, frame.y + diag + nv - mp1);
// The end partition of the last block for each merge operation is computed
// and stored as the begin partition for the subsequent merge. i.e. it is
// the same partition but in the wrong coordinate system, so its 0 when it
// should be listSize. Correct that by checking if this is the last block
// in this merge operation.
if(coop - 1 == ((coop - 1) & block)) {
a1 = min(count, frame.x + frame.z);
b1 = min(count, frame.y + frame.z);
}
return make_int4(a0, a1, b0, b1);
}For clarity and maintainability, we factor out mergesort's list-making logic into FindMergesortFrame and FindMergesortInterval. The former finds the start of the A list by masking out the bits below coop and multiplying by the grain size (either NV, or VT, depending on context). The latter function uses the intersections of the cross-diagonals with the Merge Path to calculate a CTA's or thread's input range within the provided A and B lists.
MGPU_HOST_DEVICE int4 ComputeMergeRange(int aCount, int bCount, int block,
int coop, int NV, const int* mp_global) {
// Load the merge paths computed by the partitioning kernel.
int mp0 = mp_global[block];
int mp1 = mp_global[block + 1];
int gid = NV * block;
// Compute the ranges of the sources in global memory.
int4 range;
if(coop) {
int3 frame = FindMergesortFrame(coop, block, NV);
range = FindMergesortInterval(frame, coop, block, NV, aCount, mp0,
mp1);
} else {
range.x = mp0; // a0
range.y = mp1; // a1
range.z = gid - range.x; // b0
range.w = min(aCount + bCount, gid + NV) - range.y; // b1
}
return range;
}ComputeMergeRange is the range-calculating entry point for merge, mergesort, segmented and locality sorts. This is called at the top of those respective kernels, and the A and B input-list intervals are loaded into shared memory. This unified function reduces the number of kernels needed to support this diversity of functionality.
template<typename Tuning, bool HasValues, bool MergeSort, typename KeysIt1,
typename KeysIt2, typename KeysIt3, typename ValsIt1, typename ValsIt2,
typename ValsIt3, typename Comp>
MGPU_LAUNCH_BOUNDS void KernelMerge(KeysIt1 aKeys_global, ValsIt1 aVals_global,
int aCount, KeysIt2 bKeys_global, ValsIt2 bVals_global, int bCount,
const int* mp_global, int coop, KeysIt3 keys_global, ValsIt3 vals_global,
Comp comp) {
typedef MGPU_LAUNCH_PARAMS Params;
typedef typename std::iterator_traits<KeysIt1>::value_type KeyType;
typedef typename std::iterator_traits<ValsIt1>::value_type ValType;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
union Shared {
KeyType keys[NT * (VT + 1)];
int indices[NV];
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
int4 range = ComputeMergeRange(aCount, bCount, block, coop, NT * VT,
mp_global);
DeviceMerge<NT, VT, HasValues>(aKeys_global, aVals_global, bKeys_global,
bVals_global, tid, block, range, shared.keys, shared.indices,
keys_global, vals_global, comp);
}KernelMerge is called by both the Merge and Mergesort host functions. Mergesort is considerably more involved, but this complexity has been factored out into ComputeMergeRange, allowing the heavy lifting for both functions to be defined by DeviceMerge. Note that the keys and indices are unioned in shared memory, so as to not waste resources. This is an idiom used throughput Modern GPU, and an important one to follow if your goal is high throughput.
template<int NT, MgpuBounds Bounds, typename It1, typename It2, typename Comp>
__global__ void KernelMergePartition(It1 a_global, int aCount, It2 b_global,
int bCount, int nv, int coop, int* mp_global, int numSearches, Comp comp) {
int partition = NT * blockIdx.x + threadIdx.x;
if(partition < numSearches) {
int a0 = 0, b0 = 0;
int gid = nv * partition;
if(coop) {
int3 frame = FindMergesortFrame(coop, partition, nv);
a0 = frame.x;
b0 = min(aCount, frame.y);
bCount = min(aCount, frame.y + frame.z) - b0;
aCount = min(aCount, frame.x + frame.z) - a0;
// Put the cross-diagonal into the coordinate system of the input
// lists.
gid -= a0;
}
int mp = MergePath<Bounds>(a_global + a0, aCount, b_global + b0, bCount,
min(gid, aCount + bCount), comp);
mp_global[partition] = mp;
}
}
template<MgpuBounds Bounds, typename It1, typename It2, typename Comp>
MGPU_MEM(int) MergePathPartitions(It1 a_global, int aCount, It2 b_global,
int bCount, int nv, int coop, Comp comp, CudaContext& context) {
const int NT = 64;
int numPartitions = MGPU_DIV_UP(aCount + bCount, nv);
int numPartitionBlocks = MGPU_DIV_UP(numPartitions + 1, NT);
MGPU_MEM(int) partitionsDevice = context.Malloc<int>(numPartitions + 1);
KernelMergePartition<T, Bounds>
<<<numPartitionBlocks, NT, 0, context.Stream()>>>(a_global, aCount,
b_global, bCount, nv, coop, partitionsDevice->get(), numPartitions + 1,
comp);
return partitionsDevice;
}KernelMergePartition performs coarse-granularity partitioning for both MGPU Merge and Mergesort. It fills out the mp_global Merge Path/cross-diagonal intersections that are consumed by ComputeMergeRange. This is a simple and efficient division of labor—coarse-grained scheduling is achieved by first calling MergePathPartitions to fill out mp_global, which is subsequently provided to ComputeMergeRange in an algorithm's kernel.
The MergePathPartitions function is central to the MGPU library. The argument nv is the granularity of the partition and typically is set to the number of values per CTA, NV, a product of LaunchBoxVT parameters VT and NT, and a template argument for most of MGPU's kernels. coop is the number of CTAs cooperating to merge pairs of sorted lists in the mergesort routine—this is non-zero for all other functions (like merge, vectorized sorted search, etc.).
The list of callers of MergePathPartitions is extensive:
Bulk Insert. Bulk Remove uses a standard binary search for global partitioning.
Vectorized sorted search calls both the lower- and upper-bound specializations of MergePathPartitions.
Load-balancing search calls the upper-bound function and only specializes on integer types. Additionally, all load-balancing search clients use MergePathPartitions indirectly:
Other methods don't call MergePathPartitions, but still opt into this two-phase scheduling and sequential-work approach:
The high-performance segmented and locality sorts of the next section fuse coarse-grained partitioning with work queueing, exploiting the sortedness of inputs to reduce processing.
MGPU Multisets introduce a new partitioning search called Balanced Path which incorporates duplicate ranking into key ordering. Four serial set functions, modeled after SerialMerge, perform C++-style set intersection, union, difference, and symmetric difference.
Mergesort is a multi-pass, out-of-place algorithm. The blocksort reduces global memory traffic by sorting blocks of NV elements locally, performing key exchange through low-latency shared memory. Subsequent global merge passes recursively doubles the length of sorted lists, from NV to 2*NV to 4*NV, etc., until the input is fully sorted.
template<typename T, typename Comp>
MGPU_HOST void MergesortKeys(T* data_global, int count, Comp comp,
CudaContext& context) {
const int NT = 256;
const int VT = 7;
typedef LaunchBoxVT<NT, VT> Tuning;
int2 launch = Tuning::GetLaunchParams(context);
const int NV = launch.x * launch.y;
int numBlocks = MGPU_DIV_UP(count, NV);
int numPasses = FindLog2(numBlocks, true);
MGPU_MEM(T) destDevice = context.Malloc<T>(count);
T* source = data_global;
T* dest = destDevice->get();
KernelBlocksort<Tuning, false>
<<<numBlocks, launch.x, 0, context.Stream()>>>(source, (const int*)0,
count, (1 & numPasses) ? dest : source, (int*)0, comp);
if(1 & numPasses) std::swap(source, dest);
for(int pass = 0; pass < numPasses; ++pass) {
int coop = 2<< pass;
MGPU_MEM(int) partitionsDevice = MergePathPartitions<MgpuBoundsLower>(
source, count, source, 0, NV, coop, comp, context);
KernelMerge<Tuning, false, true>
<<<numBlocks, launch.x, 0, context.Stream()>>>(source,
(const int*)0, count, source, (const int*)0, 0,
partitionsDevice->get(), coop, dest, (int*)0, comp);
std::swap(dest, source);
}
}We allocate a temporary buffer to ping-pong mergesort passes. The number of global passes is the ceil of log2 of the tile count. As the user expects results sorted in-place in data_global, we blocksort into data_global if numPasses is even and blocksort into the temporary if numPasses is odd. This way, sorted data always lands in data_global after the final merge pass without requiring an additional copy.
The mergesort host function has the same macro structure as CTABlocksortLoop: it loops from coop = 2 to coop = numBlocks (NT in blocksort). MergePathPartitions searches global memory to find the intersection of cross-diagonals and Merge Paths, as identified by the utility function FindMergesortFrame.
Idiomatic GPU codes often have this coarse-grained/fine-grained paired structure: coarse-grained partitioning and scheduling operates on the full input in global memory; fine-grained partitioning and scheduling operates on local tiles in shared memory. This simple two-level hierarchy has algorithmic benefits: the bulk of partitioning operations are run over small, constant-sized blocks, helping amortize the cost of global partitioning. We also see architecutral benefits: performing most data movement within CTAs rather than between them reduces latency and improves the throughput of kernels.