
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Replace Merge Path partitioning with the sophisticated Balanced Path to search for key-rank matches. The new partitioning strategy is combined with four different serial set operations to support CUDA analogs of std::set_intersection, set_union, set_difference, and set_symmetric_difference.

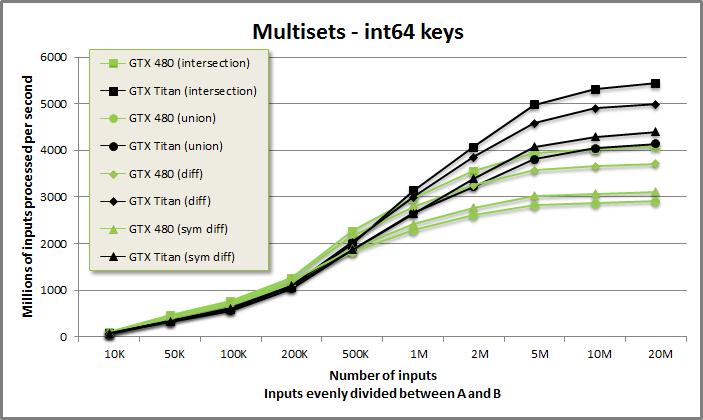
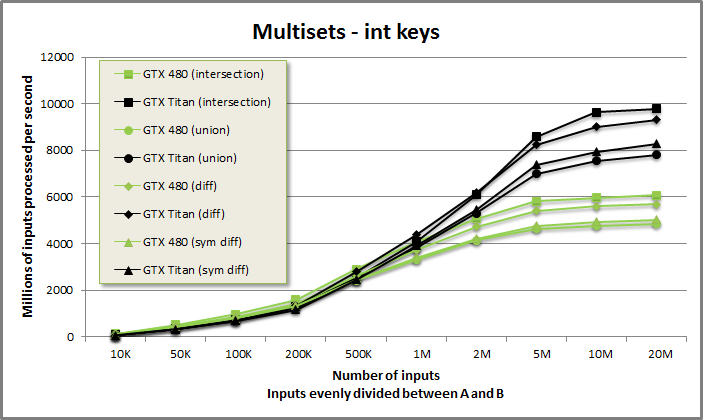
Multisets-keys benchmark from benchmarksets/benchmarksets.cu
Multisets-keys demonstration from tests/demo.cu
void DemoSets(CudaContext& context) {
printf("\nMULTISET-KEYS DEMONSTRATION:\n\n");
// Use CudaContext::SortRandom to generate 100 random sorted integers
// between 0 and 99.
int N = 100;
MGPU_MEM(int) aData = context.SortRandom<int>(N, 0, 99);
MGPU_MEM(int) bData = context.SortRandom<int>(N, 0, 99);
printf("A:\n");
PrintArray(*aData, "%4d", 10);
printf("\nB:\n\n");
PrintArray(*bData, "%4d", 10);
MGPU_MEM(int) intersectionDevice;
SetOpKeys<MgpuSetOpIntersection, true>(aData->get(), N, bData->get(), N,
&intersectionDevice, context, false);
printf("\nIntersection:\n");
PrintArray(*intersectionDevice, "%4d", 10);
MGPU_MEM(int) symDiffDevice;
SetOpKeys<MgpuSetOpSymDiff, true>(aData->get(), N, bData->get(), N,
&symDiffDevice, context, false);
printf("\nSymmetric difference:\n");
PrintArray(*symDiffDevice, "%4d", 10);
}MULTISET-KEYS DEMONSTRATION:
A:
0: 1 1 3 5 7 7 8 9 10 10
10: 10 11 12 13 14 15 16 16 16 16
20: 17 18 19 20 21 21 25 25 28 29
30: 29 29 31 31 31 31 32 33 33 35
40: 36 38 39 40 40 42 44 45 46 47
50: 47 51 51 53 53 53 55 55 56 57
60: 58 59 59 59 60 61 62 62 63 63
70: 64 68 68 70 70 72 73 73 75 78
80: 79 82 82 83 84 85 85 85 86 87
90: 89 91 91 91 92 95 97 98 98 98
B:
0: 1 2 2 3 5 6 6 9 9 10
10: 10 10 11 12 12 12 13 13 15 16
20: 16 17 17 18 21 21 22 24 25 25
30: 29 29 31 32 32 32 33 35 35 37
40: 39 39 40 41 41 42 42 44 45 46
50: 46 47 48 49 50 50 51 52 52 53
60: 54 54 54 55 56 57 59 60 65 65
70: 66 66 66 67 68 68 70 72 74 74
80: 74 74 74 75 76 76 80 82 89 89
90: 90 92 92 93 93 95 95 96 97 98
Intersection:
0: 1 3 5 9 10 10 10 11 12 13
10: 15 16 16 17 18 21 21 25 25 29
20: 29 31 32 33 35 39 40 42 44 45
30: 46 47 51 53 55 56 57 59 60 68
40: 68 70 72 75 82 89 92 95 97 98
Symmetric Difference:
0: 1 2 2 6 6 7 7 8 9 12
10: 12 13 14 16 16 17 19 20 22 24
20: 28 29 31 31 31 32 32 33 35 36
30: 37 38 39 40 41 41 42 46 47 48
40: 49 50 50 51 52 52 53 53 54 54
50: 54 55 58 59 59 61 62 62 63 63
60: 64 65 65 66 66 66 67 70 73 73
70: 74 74 74 74 74 76 76 78 79 80
80: 82 83 84 85 85 85 86 87 89 90
90: 91 91 91 92 93 93 95 96 98 98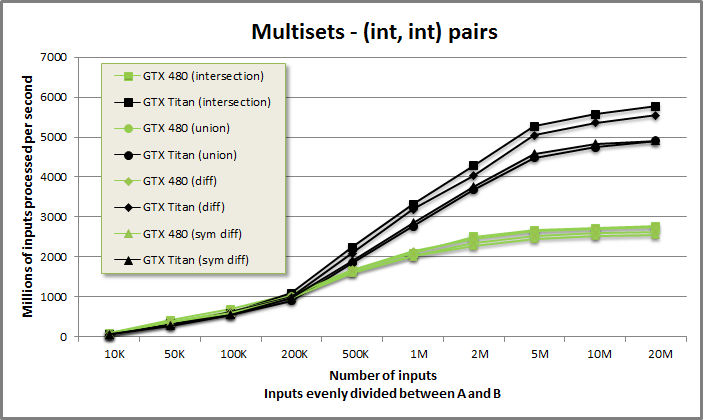
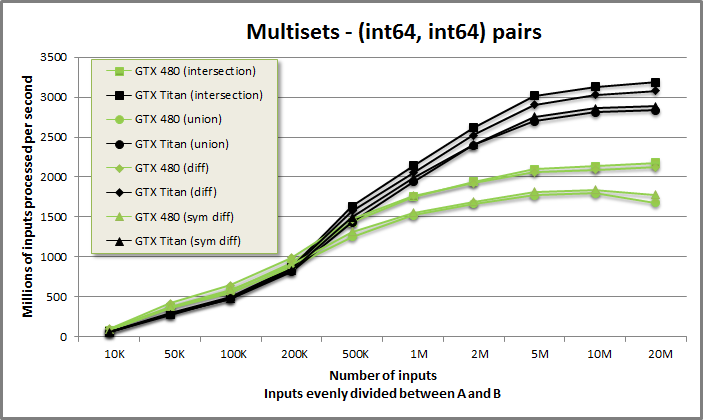
Multisets-pairs benchmark from benchmarksets/benchmarksets.cu
Multisets-pairs demonstration from tests/demo.cu
void DemoSetsPairs(CudaContext& context) {
printf("\nMULTISET-PAIRS DEMONSTRATION:\n\n");
// Use CudaContext::SortRandom to generate 100 random sorted integers
// between 0 and 99.
int N = 100;
MGPU_MEM(int) aData = context.SortRandom<int>(N, 0, 99);
MGPU_MEM(int) bData = context.SortRandom<int>(N, 0, 99);
printf("A:\n");
PrintArray(*aData, "%4d", 10);
printf("\nB:\n\n");
PrintArray(*bData, "%4d", 10);
MGPU_MEM(int) intersectionDevice, intersectionValues;
SetOpPairs<MgpuSetOpIntersection, true>(aData->get(),
mgpu::counting_iterator<int>(0), N, bData->get(),
mgpu::counting_iterator<int>(N), N, &intersectionDevice,
&intersectionValues, context);
printf("\nIntersection keys:\n");
PrintArray(*intersectionDevice, "%4d", 10);
printf("\nIntersection indices:\n");
PrintArray(*intersectionValues, "%4d", 10);
MGPU_MEM(int) symDiffDevice, symDiffValues;
SetOpPairs<MgpuSetOpSymDiff, true>(aData->get(),
mgpu::counting_iterator<int>(0), N, bData->get(),
mgpu::counting_iterator<int>(N), N, &symDiffDevice, &symDiffValues,
context);
printf("\nSymmetric difference keys:\n");
PrintArray(*symDiffDevice, "%4d", 10);
printf("\nSymmetric difference indices:\n");
PrintArray(*symDiffValues, "%4d", 10);
}MULTISET-PAIRS DEMONSTRATION:
A:
0: 0 1 1 2 3 6 6 8 11 11
10: 14 17 18 18 20 22 22 22 24 25
20: 26 27 27 31 31 31 32 33 33 34
30: 35 35 37 37 38 39 39 40 41 41
40: 42 43 44 44 44 47 50 52 56 56
50: 57 57 57 60 62 63 63 63 64 64
60: 64 65 66 67 67 68 71 72 73 75
70: 76 76 77 78 79 81 81 82 84 85
80: 85 86 86 88 89 90 91 91 91 92
90: 92 92 93 95 95 95 98 99 99 99
B:
0: 0 1 2 2 4 4 4 4 5 6
10: 6 8 8 10 10 12 13 14 18 21
20: 21 22 22 22 24 26 26 27 28 28
30: 30 32 33 34 35 38 38 38 39 40
40: 40 41 41 42 43 44 45 45 48 51
50: 53 53 53 53 54 55 57 61 61 61
60: 62 62 64 64 66 66 67 68 70 70
70: 72 74 76 78 78 79 80 80 80 80
80: 81 81 87 88 88 89 91 91 92 93
90: 93 93 94 96 97 98 98 98 98 99
Intersection keys:
0: 0 1 2 6 6 8 14 18 22 22
10: 22 24 26 27 32 33 34 35 38 39
20: 40 41 41 42 43 44 57 62 64 64
30: 66 67 68 72 76 78 79 81 81 88
40: 89 91 91 92 93 98 99
Intersection indices:
0: 0 1 3 5 6 7 10 12 15 16
10: 17 18 20 21 26 27 29 30 34 35
20: 37 38 39 40 41 42 50 54 58 59
30: 62 63 65 67 70 73 74 75 76 83
40: 84 86 87 89 92 96 97
Symmetric difference keys:
0: 1 2 3 4 4 4 4 5 8 10
10: 10 11 11 12 13 17 18 20 21 21
20: 25 26 27 28 28 30 31 31 31 33
30: 35 37 37 38 38 39 40 44 44 45
40: 45 47 48 50 51 52 53 53 53 53
50: 54 55 56 56 57 57 60 61 61 61
60: 62 63 63 63 64 65 66 67 70 70
70: 71 73 74 75 76 77 78 80 80 80
80: 80 82 84 85 85 86 86 87 88 90
90: 91 92 92 93 93 94 95 95 95 96
100: 97 98 98 98 99 99
Symmetric difference indices:
0: 2 103 4 104 105 106 107 108 112 113
10: 114 8 9 115 116 11 13 14 119 120
20: 19 126 22 128 129 130 23 24 25 28
30: 31 32 33 136 137 36 140 43 44 146
40: 147 45 148 46 149 47 150 151 152 153
50: 154 155 48 49 51 52 53 157 158 159
60: 161 55 56 57 60 61 165 64 168 169
70: 66 68 171 69 71 72 174 176 177 178
80: 179 77 78 79 80 81 82 182 184 85
90: 88 90 91 190 191 192 93 94 95 193
100: 194 196 197 198 98 99//////////////////////////////////////////////////////////////////////////////// // kernels/sets.cuh // SetOpKeys implements multiset operations with C++ set_* semantics. // MgpuSetOp may be: // MgpuSetOpIntersection - like std::set_intersection // MgpuSetOpUnion - like std::set_union // MgpuSetOpDiff - like std::set_difference // MgpuSetOpSymDiff - like std::set_symmetric_difference // Setting Duplicates to false increases performance for inputs with no // duplicate keys in either array. // The caller passes MGPU_MEM(T) pointers to hold outputs. Memory is allocated // by the multiset function using the allocator associated with the context. It // returns the number of outputs. // SetOpKeys performs one cudaMemcpyDeviceToHost to retrieve the size of // the output array. This is a synchronous operation and may prevent queueing // for callers using streams. // If compact = true, SetOpKeys pre-allocates an output buffer is large as the // sum of the input arrays. Partials results are computed into this temporary // array before being moved into the final array. It consumes more space but // results in higher performance. template<MgpuSetOp Op, bool Duplicates, typename It1, typename It2, typename T, typename Comp> MGPU_HOST int SetOpKeys(It1 a_global, int aCount, It2 b_global, int bCount, MGPU_MEM(T)* ppKeys_global, Comp comp, CudaContext& context, bool compact = true); // Specialization of SetOpKeys with Comp = mgpu::less<T>. template<MgpuSetOp Op, bool Duplicates, typename It1, typename It2, typename T> MGPU_HOST int SetOpKeys(It1 a_global, int aCount, It2 b_global, int bCount, MGPU_MEM(T)* ppKeys_global, CudaContext& context, bool compact = true); // SetOpPairs runs multiset operations by key and supports value exchange. template<MgpuSetOp Op, bool Duplicates, typename KeysIt1, typename KeysIt2, typename ValsIt1, typename ValsIt2, typename KeyType, typename ValType, typename Comp> MGPU_HOST int SetOpPairs(KeysIt1 aKeys_global, ValsIt1 aVals_global, int aCount, KeysIt2 bKeys_global, ValsIt2 bVals_global, int bCount, MGPU_MEM(KeyType)* ppKeys_global, MGPU_MEM(ValType)* ppVals_global, Comp comp, CudaContext& context); // Specialization of SetOpPairs with Comp = mgpu::less<T>. template<MgpuSetOp Op, bool Duplicates, typename KeysIt1, typename KeysIt2, typename ValsIt1, typename ValsIt2, typename KeyType, typename ValType> MGPU_HOST int SetOpPairs(KeysIt1 aKeys_global, ValsIt1 aVals_global, int aCount, KeysIt2 bKeys_global, ValsIt2 bVals_global, int bCount, MGPU_MEM(KeyType)* ppKeys_global, MGPU_MEM(ValType)* ppVals_global, CudaContext& context);
The C++ standard library includes four multiset operations: std::set_intersection, std::set_union, std::set_difference, and std::set_symmetric_difference. These functions find key-rank matches over two sorted input arrays.
Consider inputs A and B:
A: 1 1 2 3 3 3 5 6 6 6 6 7 7 8 8 9
B: 1 2 2 3 3 3 3 6 6 6 6 8
We rank the keys in each array by the order of appearance in their respective arrays:
A: 10 11 20 30 31 32 50 60 61 62 63 70 71 80 81 90
B: 10 20 21 30 31 32 33 60 61 62 63 80
Elements are placed in slots according to key-rank. Elements from both inputs that match are placed in the same slot:
| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Once the inputs are partitioned and paired, the set operations can be described and implemented by examining key-rank slots in isolation. For all operations, results are emitted from left-to-right, and each key-rank slot may generate zero or one outputs.
C++ std::set_intersection reference implementation
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_intersection (InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result)
{
while (first1!=last1 && first2!=last2)
{
if (*first1<*first2) ++first1;
else if (*first2<*first1) ++first2;
else {
*result = *first1; first2;
++result; ++first1; ++first2;
}
}
return result;
}| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-intersection selects elements in A (in green) that have no key-rank match in B. Only elements in A are returned to the caller.
C++ std::set_union reference implementation
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_union (InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result)
{
while (true)
{
if (first1==last1) return std::copy(first2,last2,result);
if (first2==last2) return std::copy(first1,last1,result);
if (*first1<*first2) { *result = *first1; ++first1; }
else if (*first2<*first1) { *result = *first2; ++first2; }
else { *result = *first1; ++first1; ++first2; }
++result;
}
}| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-union selects all elements in A plus any elements in B that have no key-rank match in A.
C++ std::set_difference reference implementation
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_difference (InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result)
{
while (first1!=last1 && first2!=last2)
{
if (*first1<*first2) { *result = *first1; ++result; ++first1; }
else if (*first2<*first1) ++first2;
else { ++first1; ++first2; }
}
return std::copy(first1,last1,result);
}
| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-difference selects only elements in A that don't have key-rank matches in B. Set-difference returns the elements in A that aren't returned by set-intersection.
C++ std::set_symmetric_difference reference implementation
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_symmetric_difference (
InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, InputIterator2 last2,
OutputIterator result)
{
while (true)
{
if (first1==last1) return std::copy(first2,last2,result);
if (first2==last2) return std::copy(first1,last1,result);
if (*first1<*first2) { *result=*first1; ++result; ++first1; }
else if (*first2<*first1) { *result = *first2; ++result; ++first2; }
else { ++first1; ++first2; }
}
}
| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-symmetric-difference selects elements in A that have no key-rank match in B and elements in B that have no key-rank match in A.
The four C++ reference codes are not obviously parallelizable. Although they appear merge-like, parallel Merge Path partitioning is inadequete. Both components of a key-rank matches must be made available to the same thread and therefore always must appear on the same side of any cross-diagonal. In the sample arrays above, Merge Path follows all four 6 keys from A before pursuing any of the 6 keys from B.
The merge order is
6a0 6a1 6a2 6a3 6b0 6b1 6b1 6b3.
We want a search that finds the intersection of cross-diagonals with a path which interleaves key-rank matches:
6a0 6b0 6a1 6b1 6a2 6b2 6a3 6b3.
Isolating the discovering of key-rank matches to partitioning code helps us cleanly separate scheduling logic from multiset logic (code resembling the C++ reference implementations from above). This has been a theme of all MGPU algorithms.
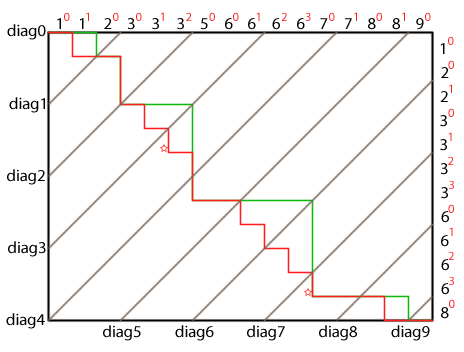
The green line in this figure is the now-familiar Merge Path. It greedily consumes all duplicates from A (the long right-directed segments) and then consumes all duplicates from B (the long down-directed segments). The red line is our answer for multiset-like problems: Balanced Path. This curve pairs all inputs by key-rank match.
To satisfy our partitioning requirements, finding the intersection of the Balanced Path with cross-diagonals is not sufficient. We must also introduce the concept of starred diagonals.
Consider diag6 in this figure. It cuts the Balanced Path putting key-rank pair (6a1, 6b1) on the left and key-rank pair (6a2, 6b2) on the right. This is proper behavior, as the partition to the left is assigned both parts of the key-rank pair 61 and the partition on the right is assigned both parts of key-rank pair 62.
diag7, on the other hand, intersects the Balanced Path between elements 6a3 and 6b3. This violates multisets' partitioning conditions: the operation-specific logic is constructed with the requirement that each CTA or thread is given both parts of all key-rank matches. To satisfy this we star the offending cross-diagonal, causing the partition on the left to steal the next element in B (on the right side of the cross-diagonal) if it's a key-rank match for the last element in A (on the left side of the cross-diagonal). Starring diag7 assigns four elements to the partition (diag6, diag7) and only two elements to the partition (diag7, diag8). Balanced Path partitions aren't precisely equal in size, but they deviate from the target grain size by only ±1.
Important: Like Merge Path, this new Balanced Path curve is constructed sequentially. We are interested in finding the intersection of the Balanced Path with a cross-diagonal without actually constructing the Balanced Path. We start by finding the intersection of the cross-diagonal with the Merge Path for the same data. Establishing this, additional searches locate where the Merge Path and Balanced Path most recently diverged. We then forward project from this point onto the cross-diagonal to complete the partitioning search.
This is an intricate task, but fortunately there is a simple geometrically-motivated algorithm:
Find the intersection of the cross-diagonal with the Merge Path (the curve in green).
Read the key in the B array at the point of intersection. If the cross-diagonal intersects a run of duplicates, it will be a run of elements with this key, because Merge Path consumes all duplicates from A before any in B.
Binary search to find the first occurrence of this key in arrays A and B—this is the position where the Balanced Path diverges from the Merge Path. In the figure, diag3 intersects the cross-diagonal where the A cursor points to 5a0 and the B cursor to 3b0. The B key is 3. Binary searching for the lower-bound of 3 into both arrays reveals the point of divergence at (3, 3), or where diag2 intersects the Merge Path.
Use the distance between the intersection computed in 1 and the divergence point in 3 to establish the duplicate run length. Project the Balanced Path (the curve in red) from the point of divergence along this run length, creating a stair-step pattern by dividing the run length evenly over A and B intervals.
We can't advance the A and B cursors evenly if the run length is odd. If this projection would separate a key-rank match, putting the A match on the left and the B match on the right of the cross-diagonal, we star the cross-diagonal, instructing the left partition to steal the B match and the right partition to cede it.
template<bool Duplicates, typename IntT, typename InputIt1, typename InputIt2,
typename Comp>
MGPU_HOST_DEVICE int2 BalancedPath(InputIt1 a, int aCount, InputIt2 b,
int bCount, int diag, int levels, Comp comp) {
typedef typename std::iterator_traits<InputIt1>::value_type T;
int p = MergePath<MgpuBoundsLower>(a, aCount, b, bCount, diag, comp);
int aIndex = p;
int bIndex = diag - p;
bool star = false;
if(bIndex < bCount) {
if(Duplicates) {
T x = b[bIndex];
// Search for the beginning of the duplicate run in both A and B.
// Because
int aStart = BiasedBinarySearch<MgpuBoundsLower, IntT>(a, aIndex, x,
levels, comp);
int bStart = BiasedBinarySearch<MgpuBoundsLower, IntT>(b, bIndex, x,
levels, comp);
// The distance between the merge path and the lower_bound is the
// 'run'. We add up the a- and b- runs and evenly distribute them to
// get a stairstep path.
int aRun = aIndex - aStart;
int bRun = bIndex - bStart;
int xCount = aRun + bRun;
// Attempt to advance b and regress a.
int bAdvance = max(xCount>> 1, xCount - aRun);
int bEnd = min(bCount, bStart + bAdvance + 1);
int bRunEnd = BinarySearch<MgpuBoundsUpper>(b + bIndex,
bEnd - bIndex, x, comp) + bIndex;
bRun = bRunEnd - bStart;
bAdvance = min(bAdvance, bRun);
int aAdvance = xCount - bAdvance;
bool roundUp = (aAdvance == bAdvance + 1) && (bAdvance < bRun);
aIndex = aStart + aAdvance;
if(roundUp) star = true;
} else {
if(aIndex && aCount) {
T aKey = a[aIndex - 1];
T bKey = b[bIndex];
// If the last consumed element in A (aIndex - 1) is the same as
// the next element in B (bIndex), we're sitting at a starred
// partition.
if(!comp(aKey, bKey)) star = true;
}
}
}
return make_int2(aIndex, star);
}BalancedPath returns the intersection of the cross-diagonal diag and the Balanced Path for input arrays a and b in .x, and the star status of the intersection in .y. When Duplicates is true, we closely follow the five steps already listed. (aIndex, bIndex) is the coordinate of the cross-diagonal intersection with the Merge Path. Binary searches on A and B returns the point of divergence with the Balanced Path at (aStart, bStart).
The function attemps to evenly distribute the total run length xCount over both inputs. However it can only distribute within duplicate runs of the sought-for key x. It runs a third binary search, an upper-bound, to find the last occurrence of the key in A. If the number of duplicates of x in A is less than half the distance from the divergence point to the cross-diagonal's intersection with the Merge Path, we project the Balanced Path only to the end of A's duplicate run and distribute the remainder of A's half to B. Graphically this keeps the red stair-step Balanced Path bounded on the top and to the right by the green Merge Path. In the figure, if we were to blindly project a stair-step path from the intersection of diag2 with the Merge Path, we'd violate key-rank ordering where diag3 happens to intersect the Merge Path: 5a0 would be consumed prior to 3b3.
FindSetPartition, the multisets counterpart to MergePathPartitions, moves the starred flag into the most-significant bit of the index when executing a global partitioning pass.
template<MgpuBounds Bounds, typename IntT, typename It, typename T,
typename Comp>
MGPU_HOST_DEVICE void BinarySearchIt(It data, int& begin, int& end, T key,
int shift, Comp comp) {
IntT scale = (1<< shift) - 1;
int mid = (int)((begin + scale * end)>> shift);
T key2 = data[mid];
bool pred = (MgpuBoundsUpper == Bounds) ?
!comp(key, key2) :
comp(key2, key);
if(pred) begin = mid + 1;
else end = mid;
}
template<MgpuBounds Bounds, typename IntT, typename T, typename It,
typename Comp>
MGPU_HOST_DEVICE int BiasedBinarySearch(It data, int count, T key, int levels,
Comp comp) {
int begin = 0;
int end = count;
if(levels >= 4 && begin < end)
BinarySearchIt<Bounds, IntT>(data, begin, end, key, 9, comp);
if(levels >= 3 && begin < end)
BinarySearchIt<Bounds, IntT>(data, begin, end, key, 7, comp);
if(levels >= 2 && begin < end)
BinarySearchIt<Bounds, IntT>(data, begin, end, key, 5, comp);
if(levels >= 1 && begin < end)
BinarySearchIt<Bounds, IntT>(data, begin, end, key, 4, comp);
while(begin < end)
BinarySearchIt<Bounds, int>(data, begin, end, key, 1, comp);
return begin;
}The cost of launching two conventional binary searches in addition to the Merge Path inside BalancedPath would be very high. If both input arrays have 10 million elements, and the intersection of the center cross-diagonal at 10 million with the Merge Path splits both arrays in half at 5 million, it hardly makes sense to run a conventional binary search over (0, 5000000) on both arrays to find the first occurrence of key x. Each search has 23 levels of depth, a heavy price to pay for key ranking. These multset functions assume that the number of duplicates in a run is much smaller than the length of the inputs; i.e., the first occurrence is, on average, close to the intersection of the cross-diagonal with the Merge Path, no matter where that intersection is. (It's unlikely that the user would want to run multiset operations on arrays with many thousands of duplicates of each key.)
We start with the interval (0, 5000000), but rather than splitting at the middle, we split 511/512ths of the way to the right, at 4990234. If there are fewer than 9766 duplicates of x in the array (highly likely), the begin iterator is advanced to 49909235—this gamble saved us 8 levels of binary searching. Otherwise we search again at (0, 4990234).
On the next level, we split the interval (0, 4990234) 127/128ths of the way to the right, at 4999923. If the first occurence of x is to the right of this (meaning there are fewer than 77 duplicates), we set begin to 4999924 and have saved another 6 levels of searching.
This strategy is called BiasedBinarySearch. When executed on data in a CTA's shared memory, two biased iterations are run before the dynamic loop of symmetric iterations, with weights 31/32 and 15/16. For global memory searches, we run four searches: 511/512, 127/128, 31/32, and 15/16 before entering the dynamic loop of symmetric searches.
To avoid undesirable division, we multiply the end iterator by 511 and add it to the left iterator, then shift 9 bits to simulate division. The multiplication may cause an overflow during searches into global memory, where the input arrays are large compared to the capacity of 32-bit ints. Biased search uses 64-bit integers to accommodate the need for more bits during midpoint calculation, but only during global search, when overflow is acutally possible. When called from the global partitioning kernel, BalancedPath is specialized with IntT = int64 and passed levels = 4, to use wide multiplication and more aggressive biasing. When called from the intra-CTA multisets function, BalancedPath is specialized with IntT = int and passed levels = 2.
BalancedPath partitions global data into NV±1-sized tiles. These intervals are loaded into CTA shared memory and further partitioned into VT±1-sized chunks. Just as we have SerialMerge to merge short intervals from shared memory into register, we have four serial set functions to read key-rank pairs from shared memory and produce results into register.
CUDA serial set-intersection from include/device/serialsets.cuh
template<int VT, bool RangeCheck, typename T, typename Comp>
MGPU_DEVICE int SerialSetIntersection(const T* data, int aBegin, int aEnd,
int bBegin, int bEnd, int end, T* results, int* indices, Comp comp) {
const int MinIterations = VT / 2;
int commit = 0;
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool test = RangeCheck ?
((aBegin + bBegin < end) && (aBegin < aEnd) && (bBegin < bEnd)) :
(i < MinIterations || (aBegin + bBegin < end));
if(test) {
T aKey = data[aBegin];
T bKey = data[bBegin];
bool pA = comp(aKey, bKey);
bool pB = comp(bKey, aKey);
// The outputs must come from A by definition of set interection.
results[i] = aKey;
indices[i] = aBegin;
if(!pB) ++aBegin;
if(!pA) ++bBegin;
if(pA == pB) commit |= 1<< i;
}
}
return commit;
}| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
For a full tile, the number of inputs equals VT±1. When key-rank elements are arranged in slots, as above, each iteration of the serial set operation advances exactly one slot, and increments one or both input pointers. Because we don't know a priori how many outputs a thread generates, each iteration stores the result (there can be no more than one result per slot) to results[i] and sets the i'th bit in the commit bitfield. After the loop has ended, each thread will count its outputs, cooperatively scan them, and compact into shared memory. This technique lets us load keys from shared memory (we need dynamic indexing, so that much is a requirement) and store to register (indexing into the output arrays is static thanks to loop unrolling by the template argument VT).
If we're processing a full tile and the caller is able to load one additional element from both A and B arrays, the four serial set ops are specialized with RangeCheck = false. In this case the function knows it won't be dealing with the end of the array and can elide range-checking tests. This reduces latency in the function, and because the kernel is intentionally underoccupied (we jack VT up to amortize the expensive Balanced Path intersection searches), it significantly boosts performance.
SerialSetIntersection takes indices (aBegin, bBegin) to the start of the thread's partition in shared memory. (aEnd, bEnd) are indices to the end of the tile's A and B intervals in shared memory. end is passed as aBegin + bBegin + partition size. This lets us check if we've consumed all the inputs for the entire partition with just a single comparison, no matter the state that the set operation takes us to.
Each thread makes exactly VT iterations through the inner loop, although as few as VT / 2 actually perform key comparisons. If the cross-diagonal on the left is starred, and the cross-diagonal on the right isn't, the thread has VT - 1 inputs. If VT = 11, there are minimally 10 elements per thread (for a full tile), and if all inputs are paired, there are only 5 active slots. So the first 5 iterations, 0-4, are executed unconditionally, and the next six, 5-10, execute only if aBegin + bBegin < end is true.
The actual logic for multiset operations is very simple:
Load the next keys from A and B into aKey and bKey.
Evaluate aKey < bKey and bKey < aKey.
Speculatively store A into the results array—all results in set-intersection come from A, and an iteration's bit in the commit bitfield must be set for the result to be compacted.
Advance the indices to the next key-rank slot. If aKey <= bKey (i.e. !comp(bKey, aKey)), increment aBegin. If bKey <= aKey (i.e. !comp(aKey, bKey)), increment bBegin.
If the set condition was satisfied, set bit i in commit to commit the result. In the case of set-intersection, both elements must make a key-rank match. We've already compared both keys against each other, and want to emit if they're equal. Predicates pA and pB can both be false (indicating equality), but they can't both be true (indicating A < B and B < A). For set-intersection we set the commit bit if pA == pB.
CUDA serial set-union from include/device/serialsets.cuh
template<int VT, bool RangeCheck, typename T, typename Comp>
MGPU_DEVICE int SerialSetUnion(const T* data, int aBegin, int aEnd,
int bBegin, int bEnd, int end, T* results, int* indices, Comp comp) {
const int MinIterations = VT / 2;
int commit = 0;
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool test = RangeCheck ?
(aBegin + bBegin < end) :
(i < MinIterations || (aBegin + bBegin < end));
if(test) {
T aKey = data[aBegin];
T bKey = data[bBegin];
bool pA = false, pB = false;
if(RangeCheck && aBegin >= aEnd)
pB = true;
else if(RangeCheck && bBegin >= bEnd)
pA = true;
else {
// Both are in range.
pA = comp(aKey, bKey);
pB = comp(bKey, aKey);
}
// Output A in case of a tie, so check if b < a.
results[i] = pB ? bKey : aKey;
indices[i] = pB ? bBegin : aBegin;
if(!pB) ++aBegin;
if(!pA) ++bBegin;
commit |= 1<< i;
}
}
return commit;
}| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
The range-checking logic is basically the same for all four serial set op functions. The material difference is how results are selected and committed. If both keys are in-range, SerialSetUnion compares them and sets the result to A, or B if B is smaller. One value from each key-rank slot is always emitted, so the commit flag is set unconditionally.
CUDA serial set-difference from include/device/serialsets.cuh
template<int VT, bool RangeCheck, typename T, typename Comp>
MGPU_DEVICE int SerialSetDifference(const T* data, int aBegin, int aEnd,
int bBegin, int bEnd, int end, T* results, int* indices, Comp comp) {
const int MinIterations = VT / 2;
int commit = 0;
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool test = RangeCheck ?
(aBegin + bBegin < end) :
(i < MinIterations || (aBegin + bBegin < end));
if(test) {
T aKey = data[aBegin];
T bKey = data[bBegin];
bool pA = false, pB = false;
if(RangeCheck && aBegin >= aEnd)
pB = true;
else if(RangeCheck && bBegin >= bEnd)
pA = true;
else {
pA = comp(aKey, bKey);
pB = comp(bKey, aKey);
}
// The outputs must come from A by definition of set difference.
results[i] = aKey;
indices[i] = aBegin;
if(!pB) ++aBegin;
if(!pA) ++bBegin;
if(pA) commit |= 1<< i;
}
}
return commit;
}
| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-difference is the complement of set-intersection. The result is unconditionally set to the A element and committed if aKey < bKey.
CUDA serial set-symmetric difference from include/device/serialsets.cuh
template<int VT, bool RangeCheck, typename T, typename Comp>
MGPU_DEVICE int SerialSetSymDiff(const T* data, int aBegin, int aEnd,
int bBegin, int bEnd, int end, T* results, int* indices, Comp comp) {
const int MinIterations = VT / 2;
int commit = 0;
#pragma unroll
for(int i = 0; i < VT; ++i) {
bool test = RangeCheck ?
(aBegin + bBegin < end) :
(i < MinIterations || (aBegin + bBegin < end));
if(test) {
T aKey = data[aBegin];
T bKey = data[bBegin];
bool pA = false, pB = false;
if(RangeCheck && (bBegin >= bEnd))
pA = true;
else if(RangeCheck && (aBegin >= aEnd))
pB = true;
else {
pA = comp(aKey, bKey);
pB = comp(bKey, aKey);
}
results[i] = pA ? aKey : bKey;
indices[i] = pA ? aBegin : bBegin;
if(!pA) ++bBegin;
if(!pB) ++aBegin;
if(pA != pB) commit |= 1<< i;
}
}
return commit;
}
| A: | 10 | 11 | 20 | 30 | 31 | 32 | 50 | 60 | 61 | 62 | 63 | 70 | 71 | 80 | 81 | 90 | ||
| B: | 10 | 20 | 21 | 30 | 31 | 32 | 33 | 60 | 61 | 62 | 63 | 80 |
Set-symmetric difference uses the identical range-checking expressions as set-difference. However instead of conditionally emitting A, it emits A or B, whichever is smaller. If the keys are equal, the function moves to the next key-rank frame.
template<int NT, int VT, MgpuSetOp Op, bool Duplicates, typename InputIt1,
typename InputIt2, typename T, typename Comp>
MGPU_DEVICE int DeviceComputeSetAvailability(InputIt1 a_global, int aCount,
InputIt2 b_global, int bCount, const int* bp_global, Comp comp,
int tid, int block, T* results, int* indices, int4& range,
bool& extended, T* keys_shared) {
const int NV = NT * VT;
int gid = NV * block;
int bp0 = bp_global[block];
int bp1 = bp_global[block + 1];
// Compute the intervals into the two source arrays.
int a0 = 0x7fffffff & bp0;
int a1 = 0x7fffffff & bp1;
int b0 = gid - a0;
int b1 = min(aCount + bCount, gid + NV) - a1;
// If the most sig bit flag is set, we're dealing with a 'starred' diagonal
// that shifts the point of intersection up.
int bit0 = (0x80000000 & bp0) ? 1 : 0;
int bit1 = (0x80000000 & bp1) ? 1 : 0;
b0 += bit0;
b1 += bit1;
// Attempt to load an 'extended' frame by grabbing an extra value from each
// array.
int aCount2 = a1 - a0;
int bCount2 = b1 - b0;
extended = (a1 < aCount) && (b1 < bCount);
int bStart = aCount2 + (int)extended;
DeviceLoad2ToShared<NT, VT, VT + 1>(a_global + a0, aCount2 + (int)extended,
b_global + b0, bCount2 + (int)extended, tid, keys_shared);
int count = aCount2 + bCount2;
// Run a Balanced Path search for each thread's starting point.
int diag = min(VT * tid - bit0, count);
int2 bp = BalancedPath<Duplicates, int>(keys_shared, aCount2,
keys_shared + bStart, bCount2, diag, 2, comp);
int a0tid = bp.x;
int b0tid = VT * tid + bp.y - bp.x - bit0;
int commit;
if(extended)
commit = SerialSetOp<VT, false, Op>(keys_shared, a0tid, aCount2,
bStart + b0tid, bStart + bCount2, bp.y, results, indices, comp);
else
commit = SerialSetOp<VT, true, Op>(keys_shared, a0tid, aCount2,
bStart + b0tid, bStart + bCount2, bp.y, results, indices, comp);
range = make_int4(a0, a1, b0, b1);
return commit;
}Threads load the tile's Balanced Path intersections and extract the source list ranges (a0, a1) and (b0, b1). Note that a star flag causes an increment to the B component of each intersection.
Due to the relative complexity of the serial set operations, we attempt to load an extra element in A and B. If this succeeds we can elide range-checking logic because we are guaranteed of not running off the end of the arrays in shared memory. This optimization is also used in the vectorized sorted search. The MGPU kernels tend to run underoccupied on current generation hardware, and reducing predicate latency often outweighs the costs of the additional global loads.
The remaining code resembles DeviceMergeKeysIndices of MGPU Merge. BalancedPath finds the starting positions for serial set ops for each thread. As with Merge the results and indices are computed into register. However because multiset operations generate a data-dependent number of outputs, we return a bitfield commit that encodes the validity of each result. Results are compacted over this bitfield by the kernel.
The MGPU Multisets function SetOpKeys has two modes of operation:
If compact = false:
KernelSetOp is launched with Stage = 0. This fully processes the input arrays, counts the outputs for each tile, and discards the results. Each tile stores its output count to global memory.
The caller scans the output counts and uses the reduction to allocate exact space for the globally-compact results.
KernelSetOp is launched with Stage = 1. This makes a second pass over the input arrays. The results are now compacted within the tile and cooperatively stored to the destination buffer.
If compact = true:
The host function allocates a temporary buffer large enough to hold all the inputs.
KernelSetOp is launched with Stage = 2. This compacts multiset results within tiles and stores the results to the temporary buffer at tile offsets. Each tile stores its output count to global memory.
The caller scans the output counts and uses the reduction to allocate exact space for the globally-compacted results.
The host launches KernelSetCompact to compact tiles of results from the temporary buffer into the destination buffer.
Compaction behavior is more efficient because the input arrays are processed only once, but it requires a lot of temporary storage. This is the default mode for StreamOpKeys (the keys-only multiset function). The compaction mode is not available for StreamOpPairs: we'd need two temporary buffers (for keys and values), and would have to copy values twice, wasting both space and bandwidth. By using the count-scan-stream pattern, the first KernelSetOp launch only touches keys; the second KernelSetOp launch compacts keys and indices inside the CTA; it stores the keys then cooperatively gathers and stores values.
template<typename Tuning, MgpuSetOp Op, bool Duplicates, int Stage,
bool HasValues, typename KeysIt1, typename KeysIt2, typename KeysIt3,
typename ValsIt1, typename ValsIt2, typename ValsIt3, typename Comp>
MGPU_LAUNCH_BOUNDS void KernelSetOp(KeysIt1 aKeys_global, ValsIt1 aVals_global,
int aCount, KeysIt2 bKeys_global, ValsIt2 bVals_global, int bCount,
int* counts_global, const int* bp_global, KeysIt3 keys_global,
ValsIt3 values_global, Comp comp) {
typedef typename std::iterator_traits<KeysIt1>::value_type KeyType;
typedef typename std::iterator_traits<ValsIt1>::value_type ValType;
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
const int NV = NT * VT;
typedef CTAReduce<NT, ScanOpAdd> R;
typedef CTAScan<NT, ScanOpAdd> S;
union Shared {
KeyType keys[NT * (VT + 1)];
int indices[NV];
typename R::Storage reduce;
typename S::Storage scan;
};
__shared__ Shared shared;
int tid = threadIdx.x;
int block = blockIdx.x;
// Run the set operation. Return a bitfield for the selected keys.
KeyType results[VT];
int indices[VT];
int4 range;
bool extended;
int commit = DeviceComputeSetAvailability<NT, VT, Op, Duplicates>(
aKeys_global, aCount, bKeys_global, bCount, bp_global, comp, tid, block,
results, indices, range, extended, shared.keys);
aCount = range.y - range.x;
bCount = range.w - range.z;
// scan or reduce over the number of emitted keys per thread.
int outputCount = popc(commit);
int outputTotal;
if(0 == Stage) {
// Stage 0 - count the outputs.
outputTotal = R::Reduce(tid, outputCount, shared.reduce);
} else {
int globalStart = (1 == Stage) ? counts_global[block] : (NV * block);
// Stage 1 or 2 - stream the keys.
int scan = S::Scan(tid, outputCount, shared.scan, &outputTotal);
// Write the commit results to shared memory.
int start = scan;
#pragma unroll
for(int i = 0; i < VT; ++i)
if((1<< i) & commit)
shared.keys[start++] = results[i];
__syncthreads();
// Store keys to global memory.
DeviceSharedToGlobal<NT, VT>(outputTotal, shared.keys, tid,
keys_global + globalStart);
if(HasValues) {
// indices[] has gather indices in thread order. Compact and store
// these to shared memory for a transpose to strided order.
start = scan;
#pragma unroll
for(int i = 0; i < VT; ++i)
if((1<< i) & commit)
shared.indices[start++] = indices[i];
__syncthreads();
aVals_global += range.x;
bVals_global += range.z;
values_global += globalStart;
if(MgpuSetOpIntersection == Op || MgpuSetOpDiff == Op)
DeviceGatherGlobalToGlobal<NT, VT>(outputTotal, aVals_global,
shared.indices, tid, values_global, false);
else
DeviceTransferMergeValues<NT, VT>(outputTotal, aVals_global,
bVals_global, aCount + (int)extended, shared.indices, tid,
values_global, false);
}
}
if(1 != Stage && !tid)
counts_global[block] = outputTotal;
}Judicious factoring allows one implementation of KernelSetOp to support all three multiset launches described above. Although the function feels more like a merge, the implementation has more in common with vectorized sorted search, in that valid outputs are compacted with a loop over a commit bitfield. To copy values, we make a second loop over the set bits in commit, compact the indices of valid outputs to shared memory, and cooperatively gather and store data from values_global using these indices.
Set-union and set-symmetric difference return elements from both arrays, and for these merge-like operations we tap DeviceTransferMergeValues to facilitate the gather and store. Set-intersection and set-difference return only elements from the A input, presenting an opportunity for optimization: we call DeviceGatherGlobalToGlobal; it's similar to DeviceTransferMergeValues but drops predication by only supports a single input array.