
© 2013, NVIDIA CORPORATION. All rights reserved.
Code and text by Sean Baxter, NVIDIA Research.
(Click here for license. Click here for contact information.)
Sort-merge joins supporting inner, left, right, and outer variants. Uses vectorized sorted search to match keys between input arrays and load-balancing search to manage Cartesian products.

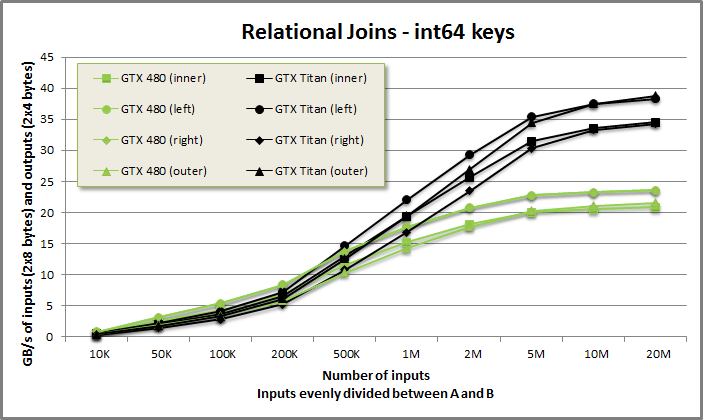
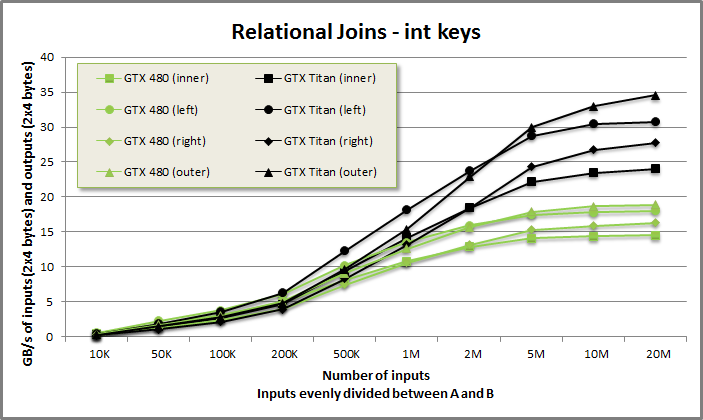
Relational joins benchmark from benchmarkjoin/benchmarkjoin.cu
Relational joins demonstration from tests/demo.cu
void DemoJoin(CudaContext& context) {
printf("RELATIONAL JOINS DEMONSTRATION\n\n");
int ACount = 30;
int BCount = 30;
MGPU_MEM(int) aKeysDevice = context.SortRandom<int>(ACount, 100, 130);
MGPU_MEM(int) bKeysDevice = context.SortRandom<int>(BCount, 100, 130);
std::vector<int> aKeysHost, bKeysHost;
aKeysDevice->ToHost(aKeysHost);
bKeysDevice->ToHost(bKeysHost);
printf("A keys:\n");
PrintArray(*aKeysDevice, "%4d", 10);
printf("\nB keys:\n");
PrintArray(*bKeysDevice, "%4d", 10);
MGPU_MEM(int) aIndices, bIndices;
int innerCount = RelationalJoin<MgpuJoinKindInner>(aKeysDevice->get(),
ACount, bKeysDevice->get(), BCount, &aIndices, &bIndices, context);
std::vector<int> aHost, bHost;
aIndices->ToHost(aHost);
bIndices->ToHost(bHost);
printf("\nInner-join (%d items):\n", innerCount);
printf("output (aIndex, bIndex) : (aKey, bKey)\n");
printf("----------------------------------------\n");
for(int i = 0; i < innerCount; ++i)
printf("%3d (%6d, %6d) : (%4d, %4d)\n", i, aHost[i], bHost[i],
aKeysHost[aHost[i]], bKeysHost[bHost[i]]);
int outerCount = RelationalJoin<MgpuJoinKindOuter>(aKeysDevice->get(),
ACount, bKeysDevice->get(), BCount, &aIndices, &bIndices, context);
aIndices->ToHost(aHost);
bIndices->ToHost(bHost);
printf("\nOuter-join (%d items):\n", outerCount);
printf("output (aIndex, bIndex) : (aKey, bKey)\n");
printf("----------------------------------------\n");
for(int i = 0; i < outerCount; ++i) {
char aKey[5], bKey[5];
if(-1 != aHost[i]) itoa(aKeysHost[aHost[i]], aKey, 10);
if(-1 != bHost[i]) itoa(bKeysHost[bHost[i]], bKey, 10);
printf("%3d (%6d, %6d) : (%4s, %4s)\n", i, aHost[i], bHost[i],
(-1 != aHost[i]) ? aKey : "---", (-1 != bHost[i]) ? bKey : "---");
}
}RELATIONAL JOINS DEMONSTRATION
A keys:
0: 100 102 103 103 103 103 103 104 104 105
10: 106 106 106 107 108 109 109 110 111 113
20: 114 114 114 116 116 116 118 119 121 127
B keys:
0: 100 101 102 102 105 105 105 105 106 107
10: 109 112 116 117 117 118 119 121 125 125
20: 126 126 126 126 128 128 128 129 130 130
Inner-join (19 items):
output (aIndex, bIndex) : (aKey, bKey)
----------------------------------------
0 ( 0, 0) : ( 100, 100)
1 ( 1, 2) : ( 102, 102)
2 ( 1, 3) : ( 102, 102)
3 ( 9, 4) : ( 105, 105)
4 ( 9, 5) : ( 105, 105)
5 ( 9, 6) : ( 105, 105)
6 ( 9, 7) : ( 105, 105)
7 ( 10, 8) : ( 106, 106)
8 ( 11, 8) : ( 106, 106)
9 ( 12, 8) : ( 106, 106)
10 ( 13, 9) : ( 107, 107)
11 ( 15, 10) : ( 109, 109)
12 ( 16, 10) : ( 109, 109)
13 ( 23, 12) : ( 116, 116)
14 ( 24, 12) : ( 116, 116)
15 ( 25, 12) : ( 116, 116)
16 ( 26, 15) : ( 118, 118)
17 ( 27, 16) : ( 119, 119)
18 ( 28, 17) : ( 121, 121)
Outer-join (50 items):
output (aIndex, bIndex) : (aKey, bKey)
----------------------------------------
0 ( 0, 0) : ( 100, 100)
1 ( 1, 2) : ( 102, 102)
2 ( 1, 3) : ( 102, 102)
3 ( 2, -1) : ( 103, ---)
4 ( 3, -1) : ( 103, ---)
5 ( 4, -1) : ( 103, ---)
6 ( 5, -1) : ( 103, ---)
7 ( 6, -1) : ( 103, ---)
8 ( 7, -1) : ( 104, ---)
9 ( 8, -1) : ( 104, ---)
10 ( 9, 4) : ( 105, 105)
11 ( 9, 5) : ( 105, 105)
12 ( 9, 6) : ( 105, 105)
13 ( 9, 7) : ( 105, 105)
14 ( 10, 8) : ( 106, 106)
15 ( 11, 8) : ( 106, 106)
16 ( 12, 8) : ( 106, 106)
17 ( 13, 9) : ( 107, 107)
18 ( 14, -1) : ( 108, ---)
19 ( 15, 10) : ( 109, 109)
20 ( 16, 10) : ( 109, 109)
21 ( 17, -1) : ( 110, ---)
22 ( 18, -1) : ( 111, ---)
23 ( 19, -1) : ( 113, ---)
24 ( 20, -1) : ( 114, ---)
25 ( 21, -1) : ( 114, ---)
26 ( 22, -1) : ( 114, ---)
27 ( 23, 12) : ( 116, 116)
28 ( 24, 12) : ( 116, 116)
29 ( 25, 12) : ( 116, 116)
30 ( 26, 15) : ( 118, 118)
31 ( 27, 16) : ( 119, 119)
32 ( 28, 17) : ( 121, 121)
33 ( 29, -1) : ( 127, ---)
34 ( -1, 1) : ( ---, 101)
35 ( -1, 11) : ( ---, 112)
36 ( -1, 13) : ( ---, 117)
37 ( -1, 14) : ( ---, 117)
38 ( -1, 18) : ( ---, 125)
39 ( -1, 19) : ( ---, 125)
40 ( -1, 20) : ( ---, 126)
41 ( -1, 21) : ( ---, 126)
42 ( -1, 22) : ( ---, 126)
43 ( -1, 23) : ( ---, 126)
44 ( -1, 24) : ( ---, 128)
45 ( -1, 25) : ( ---, 128)
46 ( -1, 26) : ( ---, 128)
47 ( -1, 27) : ( ---, 129)
48 ( -1, 28) : ( ---, 130)
49 ( -1, 29) : ( ---, 130)//////////////////////////////////////////////////////////////////////////////// // kernels/join.cuh // RelationalJoin is a sort-merge join that returns indices into one of the four // relational joins: // MgpuJoinKindInner // MgpuJoinKindLeft // MgpuJoinKindRight // MgpuJoinKindOuter. // A = 100, 101, 103, 103 // B = 100, 100, 102, 103 // Outer join: // ai, bi a[ai], b[bi] // 0: (0, 0) - (100, 100) // cross-product expansion for key 100 // 1: (0, 1) - (100, 100) // 2: (1, -) - (101, ---) // left-join for key 101 // 3: (-, 2) - (---, 102) // right-join for key 102 // 4: (3, 3) - (103, 103) // cross-product expansion for key 103 // MgpuJoinKindLeft drops the right-join on line 3. // MgpuJoinKindRight drops the left-join on line 2. // MgpuJoinKindInner drops both the left- and right-joins. // The caller passes MGPU_MEM(int) pointers to hold indices. Memory is allocated // by the join function using the allocator associated with the context. It // returns the number of outputs. // RelationalJoin performs one cudaMemcpyDeviceToHost to retrieve the size of // the output array. This is a synchronous operation and may prevent queueing // for callers using streams. template<MgpuJoinKind Kind, typename InputIt1, typename InputIt2, typename Comp> MGPU_HOST int RelationalJoin(InputIt1 a_global, int aCount, InputIt2 b_global, int bCount, MGPU_MEM(int)* ppAJoinIndices, MGPU_MEM(int)* ppBJoinIndices, Comp comp, CudaContext& context); // Specialization of RelationJoil with Comp = mgpu::less<T>. template<MgpuJoinKind Kind, typename InputIt1, typename InputIt2> MGPU_HOST int RelationalJoin(InputIt1 a_global, int aCount, InputIt2 b_global, int bCount, MGPU_MEM(int)* ppAJoinIndices, MGPU_MEM(int)* ppBJoinIndices, CudaContext& context);
Join is a foundational operation in relational algebra and relational databases. Joins take two tables and return a new table. A column from each table serves as a key and the join operator produces the Cartesian product of all rows with matching keys. MGPU Join is a merge-join that supports duplicate keys and left-, right-, and outer-join semantics.
| Row: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Table A: | A0 | A1 | B0 | E0 | E1 | E2 | E3 | F0 | F1 | G0 | H0 | H1 | J0 | J1 | M0 | M1 |
| Table B: | A0 | A1 | B0 | B1 | B2 | C0 | C1 | F0 | G0 | G1 | H0 | I0 | L0 | L1 |
Table A has 16 rows and B has 14. The key fields for the join are displayed above. The keys are sorted within each table (a requirement for merge-join) and the ranks of the keys are inferred. We join over matching letters and generate a Cartesian product for all ranks.
| Row | A index | A key | B key | B index | Join type |
| 0 | 0 | A0 | A0 | 0 | inner |
| 1 | 0 | A0 | A1 | 1 | inner |
| 2 | 1 | A1 | A0 | 0 | inner |
| 3 | 1 | A1 | A1 | 1 | inner |
| 4 | 2 | B0 | B0 | 2 | inner |
| 5 | 2 | B0 | B1 | 3 | inner |
| 6 | 2 | B0 | B2 | 4 | inner |
| 7 | 3 | E0 | --- | -1 | left |
| 8 | 4 | E1 | --- | -1 | left |
| 9 | 5 | E2 | --- | -1 | left |
| 10 | 6 | E3 | --- | -1 | left |
| 11 | 7 | F0 | F0 | 7 | inner |
| 12 | 8 | F1 | F0 | 7 | inner |
| 13 | 9 | G0 | G0 | 8 | inner |
| 14 | 9 | G0 | G1 | 9 | inner |
| 15 | 10 | H0 | H0 | 10 | inner |
| 16 | 11 | H1 | H0 | 10 | inner |
| 17 | 12 | J0 | --- | -1 | left |
| 18 | 13 | J1 | --- | -1 | left |
| 19 | 14 | M0 | --- | -1 | left |
| 20 | 15 | M1 | --- | -1 | left |
| 21 | -1 | --- | C0 | 5 | right |
| 22 | -1 | --- | C1 | 6 | right |
| 23 | -1 | --- | I0 | 11 | right |
| 24 | -1 | --- | L0 | 12 | right |
| 25 | -1 | --- | L1 | 13 | right |
Merge-join takes sorted inputs and returns an output table that is sorted first by A, and within matching A keys, by B keys.
Inner-join produces the Cartesian product of matching keys over their ranks. In this case both keys are non-null and indices are defined.
Left-join adds to inner-join the set of rows in A with keys that are unmatched in B. With left-join, all rows in the A input are included in the output. The B component of left-join tuples is a null key. MGPU Join uses the index -1 for null keys; this key is lexicographically larger than all other keys.
Right-join adds to inner-join the set of rows in B with keys that are unmatched in A. With right-join, all rows in the B input are included in the output. The A component of right-join tuples is a null key. Because outputs are sorted first by A key and then by B key, rows generated by right-join are appended to the end of the output table and are sorted by B index.
Full outer-join is the union of inner-, left-, and outer-join rows. All input rows are returned by an outer-join operation.
MGPU Join supports all four join types. It returns a dynamically-allocated set of A index/B index pairs. The caller can retrieve the joined keys with a simple gather.
The function is implemented by leaning heavily on vectorized sorted search and load-balancing search. It is decomposed into a few simple steps:
Use vectorized sorted search to find the lower-bound of A into B. For right/outer-join, also return the set of matches and the match count of B into A.
Use SortedEqualityCount to find the number of matches in B for each element in A. For left/outer-join, use the LeftJoinEqualityOp operator to always return a count of at least 1.
Scan the Cartesian-product counts in 2 and save the reduction of the counts as leftJoinTotal, which is the number of outputs contributed by the left/inner-join parts.
Add the leftJoinTotal in 3 with the right-join total in 1 (the right-join contribution is the number of elements in B that have no matches in A) and save as joinTotal. Allocate device memory to hold this many join outputs.
Run an upper-bound MergePath search as part of the load-balancing search that enables the left/inner-join implementation.
Launch KernelLeftJoin:
Run the CTALoadBalance boilerplate: rows in the A table are considered "generating objects" and outputs are work-items.
Threads locate the rank of each output within its generating object—that is, the superscript on the B key of the output. In the table above, output row 2 (A1, A0) is rank 0, because it is the first element of the Cartesian product with key A1 on the left. Output row 3 (A1, A1) is rank 1, because it is the second element of the Cartesian product with key A1 on the left. Left-join outputs always are rank 0.
Cooperatively load the lower-bound of A into B (computed in 1) into shared memory for each row of table A that is referenced inside the CTA.
Store the left/inner-join indices to global memory. The A index is the generating object's index as computed by the load-balancing search. For an inner-join, the B index is the lower-bound of A into B plus the rank of the output. For a left-join, the B index is -1, representing the null key.
For a right/outer-join, compact the indices of the rows in B that were not matched in 1 to the end of the output array. cudaMemset -1s to the corresponding A indices.
template<MgpuJoinKind Kind, typename InputIt1, typename InputIt2,
typename Comp>
MGPU_HOST int RelationalJoin(InputIt1 a_global, int aCount, InputIt2 b_global,
int bCount, MGPU_MEM(int)* ppAJoinIndices, MGPU_MEM(int)* ppBJoinIndices,
Comp comp, CudaContext& context) {
typedef typename std::iterator_traits<InputIt1>::value_type T;
const bool SupportLeft = MgpuJoinKindLeft == Kind ||
MgpuJoinKindOuter == Kind;
const bool SupportRight = MgpuJoinKindRight == Kind ||
MgpuJoinKindOuter == Kind;
const MgpuSearchType LeftType = SupportLeft ?
MgpuSearchTypeIndexMatch : MgpuSearchTypeIndex;
MGPU_MEM(int) aLowerBound = context.Malloc<int>(aCount);
MGPU_MEM(byte) bMatches;
// Find the lower bound of A into B. If we are right joining also return the
// set of matches of B into A.
int rightJoinTotal = 0;
if(SupportRight) {
// Support a right or outer join. Count the number of B elements that
// have matches in A. These matched values are included in the inner
// join part. The other values (bCount - bMatchCount) are copied to the
// end for the right join part.
bMatches = context.Malloc<byte>(bCount);
int bMatchCount;
SortedSearch<MgpuBoundsLower, LeftType, MgpuSearchTypeMatch>(a_global,
aCount, b_global, bCount, aLowerBound->get(), bMatches->get(), comp,
context, 0, &bMatchCount);
rightJoinTotal = bCount - bMatchCount;
} else
SortedSearch<MgpuBoundsLower, LeftType, MgpuSearchTypeNone>(a_global,
aCount, b_global, bCount, aLowerBound->get(), (int*)0, comp,
context, 0, 0);The host function RelationalJoin starts by calling SortedSearch to find the lower-bound of A into B. The function is specialized over one of four possible parameterizations, depending on join type.
When supporting left-join, matches of A into B are computed in addition to the lower-bound indices—matches are indicated by setting the high bit of the indices.
When supporting right-join, matches of B into A are returned in bytes. All we really need are bits, but those aren't directly addressable. The total number of matches is returned in the last SortedSearch argument; it is subtracted from the size of the B array: this is the number of right-join rows to append to the end of the output.
RelationalJoin (continued) from include/kernels/join.cuh
// Use the lower bounds to compute the counts for each element. MGPU_MEM(int) aCounts = context.Malloc<int>(aCount); if(SupportLeft) SortedEqualityCount(a_global, aCount, b_global, bCount, aLowerBound->get(), aCounts->get(), comp, LeftJoinEqualityOp(), context); else SortedEqualityCount(a_global, aCount, b_global, bCount, aLowerBound->get(), aCounts->get(), comp, SortedEqualityOp(), context); // Scan the product counts. This is part of the load-balancing search. int leftJoinTotal = Scan(aCounts->get(), aCount, context);
The second section calls SortedEqualityCount: an upper-bound of A into B is run and its different from the lower-bound in returned as a count. This is the count of B values created for each A value—the Cartesian product is implemented by generating a variable number of outputs for each individual element of A. To support left-join, we specialize with the LeftJoinEqualityOp; this returns a 1 count when there are no elements in B matching a key in A. Because the join kernel uses load-balancing search we scan the counts in-place. This creates a sorted array that can be pushed through the upper-bound MergePathPartitions.
RelationalJoin (continued) from include/kernels/join.cuh
// Allocate space for the join indices from the sum of left and right join // sizes. int joinTotal = leftJoinTotal + rightJoinTotal; MGPU_MEM(int) aIndicesDevice = context.Malloc<int>(joinTotal); MGPU_MEM(int) bIndicesDevice = context.Malloc<int>(joinTotal); // Launch the inner/left join kernel. Run an upper-bounds partitioning // to load-balance the data. const int NT = 128; const int VT = 7; typedef LaunchBoxVT<NT, VT> Tuning; int2 launch = Tuning::GetLaunchParams(context); int NV = launch.x * launch.y; MGPU_MEM(int) partitionsDevice = MergePathPartitions<MgpuBoundsUpper>( mgpu::counting_iterator<int>(0), leftJoinTotal, aCounts->get(), aCount, NV, 0, mgpu::less<int>(), context); int numBlocks = MGPU_DIV_UP(leftJoinTotal + aCount, NV); KernelLeftJoin<Tuning, SupportLeft> <<<numBlocks, launch.x, 0, context.Stream()>>>(leftJoinTotal, aLowerBound->get(), aCounts->get(), aCount, partitionsDevice->get(), aIndicesDevice->get(), bIndicesDevice->get());
A LaunchBox is created to support device-specific parameterizations. Although we launch a number of routines from RelationalJoin, we only control the tuning parameters for KernelLeftJoin—the other kernels are pre-packaged in host functions that define their own launch parameters.
Index pairs are allocated, MergePathPartitions is called to prepare the load-balancing search, and KernelLeftJoin is launched. This kernel performs both the left- and inner-join parts. Right-join is a comparatively trivial operation involving a simple index compaction to the end of the index arrays. It is saved for the end.
template<typename Tuning, bool LeftJoin>
MGPU_LAUNCH_BOUNDS void KernelLeftJoin(int total, const int* aLowerBound_global,
const int* aCountsScan_global, int aCount, const int* mp_global,
int* aIndices_global, int* bIndices_global) {
typedef MGPU_LAUNCH_PARAMS Params;
const int NT = Params::NT;
const int VT = Params::VT;
__shared__ int indices_shared[NT * (VT + 1)];
int tid = threadIdx.x;
int block = blockIdx.x;
int4 range = CTALoadBalance<NT, VT>(total, aCountsScan_global, aCount,
block, tid, mp_global, indices_shared, true);
int outputCount = range.y - range.x;
int inputCount = range.w - range.z;
int* output_shared = indices_shared;
int* input_shared = indices_shared + outputCount;
int aIndex[VT], rank[VT];
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = NT * i + tid;
if(index < outputCount) {
int gid = range.x + index;
aIndex[i] = output_shared[index];
rank[i] = gid - input_shared[aIndex[i] - range.z];
aIndices_global[gid] = aIndex[i];
}
}
__syncthreads();
// Load the lower bound of A into B for each element of A.
DeviceMemToMemLoop<NT>(inputCount, aLowerBound_global + range.z, tid,
input_shared);
// Store the lower bound of A into B back for every output.
#pragma unroll
for(int i = 0; i < VT; ++i) {
int index = NT * i + tid;
if(index < outputCount) {
int gid = range.x + index;
int lb = input_shared[aIndex[i] - range.z];
int bIndex;
if(LeftJoin)
bIndex = (0x80000000 & lb) ?
((0x7fffffff & lb) + rank[i]) :
-1;
else
bIndex = lb + rank[i];
bIndices_global[gid] = bIndex;
}
}
}The left-join kernel closely resembles Interval Move. We load-balance outputs and inputs (each input is one row of A) in shared memory. Ranks for each output are computed.
Recall the figure from the top: the A-rank of an output row is equal to the superscript of the B key. Row 6, for example, match keys "B". It is the third occurrence of B0 in A, or rank 2 (we count ranks in zero-based indexing). Therefore it must be paired with B2 in B.
Load-balancing search provides the rank of each key occurrence in A. The rank is used to infer the index of the corresponding row in B. The lower-bound of A into B, computed earlier in RelationalJoin, provides the index of the first key-match in B. We add the rank of the output into this lower-bound for B's index in the output:
bIndex = lb + rank[i]; Infer the B index from the lower-bound of A into B and the A-rank of the output row.
If the user has requested a left/outer-join we check the match bit of the lower-bound (the most significant bit), and emit the null index -1 to form a left-join output:
bIndex = (0x80000000 & lb) ? ((0x7fffffff & lb) + rank[i]) : -1; Return the B index only if this is an inner-type output, as indicated by a set match bit on the lower-bound term.
RelationalJoin (continued) from include/kernels/join.cuh
// Launch the right join kernel. Compact the non-matches from B into A.
if(SupportRight) {
const int NT = 128;
int numBlocks = MGPU_DIV_UP(bCount, 8 * NT);
MGPU_MEM(int) totals = context.Malloc<int>(numBlocks);
KernelRightJoinUpsweep<NT><<<numBlocks, NT>>>(
(const uint64*)bMatches->get(), bCount, totals->get());
Scan<MgpuScanTypeExc>(totals->get(), numBlocks, totals->get(),
ScanOpAdd(), (int*)0, false, context);
KernelRightJoinDownsweep<NT><<<numBlocks, NT>>>(
(const uint64*)bMatches->get(), bCount, totals->get(),
bIndicesDevice->get() + leftJoinTotal);
cudaMemset(aIndicesDevice->get() + leftJoinTotal, -1,
sizeof(int) * rightJoinTotal);
}
*ppAJoinIndices = aIndicesDevice;
*ppBJoinIndices = bIndicesDevice;
return joinTotal;
}The right-join code performs a simple index compaction into the end of the output arrays. KernelRightJoinUpsweep counts the number of elements in B that do not have matches in A. (Recall that we already computed the match terms into a byte array with a vectorized sorted search specialization.) The partials are scanned to find the offset within the output array for each tile to stream its indices. KernelRightJoinDownsweep revisits the match flags and streams the B indices. We finalize the relational join by setting the A indices to -1, indicating a null key and a right-join output.